题目内容
6.若两个函数y=f(x),y=g(x)在给定相同的定义域上恒有f(x)g(x)≥0,则称这两个函数是“和谐函数”,已知f(x)=ax-20,$g(x)=lg(\frac{x}{a})(a∈R)$在x∈N*上是“和谐函数”,则a的取值范围是[4,5].分析 运用对数函数的定义域可得a>0,求得f(x),g(x)的零点,由于4×5=20,讨论当0<a<4时,当a>5时,当4≤a≤5时,由不等式的性质即可得到所求范围.
解答 解:由定义域可得$\frac{x}{a}$>0,由题意可得a>0.
由f(x)=0,可得x=$\frac{20}{a}$,由g(x)=0,可得x=a.
由题意可得两零点之间无正整数,
由于4×5=20,所以当0<a<4时,$\frac{20}{a}$>5,不满足题意;
当a>5时,0<$\frac{20}{a}$<4,不满足题意;当4≤a≤5时,4≤$\frac{20}{a}$≤5,满足题意.
故答案为:[4,5].
点评 本题考查新定义的理解和运用,考查函数的零点的求法,以及转化思想,分类讨论思想,属于中档题.

练习册系列答案
相关题目
19.某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示,其中第二批次女教职工人数占总人数的16%.
(1)求x的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
| 第一批次 | 第二批次 | 第三批次 | |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
 ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( ) B.
B.
 D.
D.
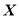 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求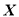 的分布列与数学期望.
的分布列与数学期望. ,并且
,并且 ,则方差
,则方差 ( )
( ) B.
B. C.
C. D.
D.