题目内容
18.求下列函数的导数.(1)y=x2sinx;
(2)y=3xex-2x+e;
(3)y=$\frac{lnx}{{x}^{2}+1}$;
(4)y=cos32x+ex.
分析 根据导数的运算法则和复合函数的求导方法求解即可.
解答 解:(1)y′=2xsinx+x2cosx;
(2)y′=3xexln3e-2xln2=3xex(ln3+1)-2xln2;
(3)y′=$\frac{\frac{1}{x}({x}^{2}+1)-2xlnx}{({x}^{2}+1)^{2}}$=$\frac{{x}^{2}-2{x}^{2}lnx+1}{x({x}^{2}+1)^{2}}$;
(4)y′=3cos22x•(-sin2x)•2+ex
=-3sin4xcos2x+ex.
点评 本题主要考查导数的运算法则和复合函数的求导方法.

练习册系列答案
相关题目
8.执行如图所示的程序框图,则输出的S的值是( )
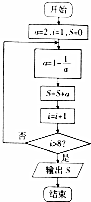

| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
9.若在区间[-1,2]中随机地取一个数x,则事件“0≤x≤2”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.在△ABC中,$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$,$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{PQ}$=( )
| A. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ |
7.已知等比数列{an}的各项均为正数,且满足a3=a1+2a2,则$\frac{{a}_{9}+{a}_{10}}{{a}_{7}+{a}_{8}}$等于( )
| A. | 2+3$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 3-2$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
3.已知a>0,且a≠1,下列函数中,在其定义域内是单调函数而且又是奇函数的是( )
| A. | y=sinax | B. | y=logax2 | C. | y=ax-a-x | D. | y=tanax |