题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,若acosB+bcosA=4cosC,且c=2,则△ABC面积的最大值为( )
A、
| ||
B、
| ||
| C、2 | ||
D、2
|
考点:两角和与差的正弦函数,正弦定理
专题:解三角形
分析:利用正弦定理把题设中关于边的等式转换成角的正弦,进而利用两角和公式化简整理求得cosC,进而求得C.根据余弦定理求得a和b的不等式关系,进而利用三角形面积公式表示出三角形的面积,利用a和b的不等式关系求得三角形面积的最大值.
解答:
解:∵acosB+bcosA=4cosC,且c=2,
∴由题意及正弦定理可得:sinAcosB+sinBcosA=2sinCcosC,
即sinC=2sinCcosC,故cosC=
,
可解得:sinC=
,
可得:cosC=
=
,
∴ab=a2+b2-4≥2ab-4,即ab≤4,等号当a=b时成立,
∴可得:S△ABC=
absinC≤
.
故选:A.
∴由题意及正弦定理可得:sinAcosB+sinBcosA=2sinCcosC,
即sinC=2sinCcosC,故cosC=
| 1 |
| 2 |
可解得:sinC=
| ||
| 2 |
可得:cosC=
| 1 |
| 2 |
| a2+b2-4 |
| 2ab |
∴ab=a2+b2-4≥2ab-4,即ab≤4,等号当a=b时成立,
∴可得:S△ABC=
| 1 |
| 2 |
| 3 |
故选:A.
点评:本题主要考查了余弦定理的应用,正弦定理的应用,两角和公式的化简求值,属于基本知识的考查.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
下列函数是以π为周期的偶函数的是( )
| A、y=tanx | ||
B、y=sin(x+
| ||
C、y=sin(2x+
| ||
D、y=cos(2x+
|
若正数a,b满足ab=a+b+8,则ab的取值范围是( )
| A、(0,16] |
| B、[4,16) |
| C、[4,16] |
| D、[16,+∞) |
直线y-5=0的斜率为( )
| A、1 | B、0 | C、5 | D、不存在 |
某中学准备从高一、高二共2014名学生中选派50名学生参加冬令营活动,若采用下面的方法选取:先用简单随机抽样的方法从2014人中剔除14人,剩下的2000人再按系统抽样的方法抽取50人,则在这2014名学生中,每个人入选的概率( )
A、都相等,且为
| ||
B、都相等,且为
| ||
| C、均不相等 | ||
| D、不全相等 |
已知命题p:“?a”的否定是“?x0<0,x02+x0-1≥0”;命题q:在△ABC中“∠A>∠B”的充要条件是“sinA>sinB”;则下列命题是假命题的是( )
| A、p∨q |
| B、p∨(?q) |
| C、(?p)∨q |
| D、(?p)∨(?q) |
已知集合M={0,1,2},N={x},若M∪N={0,1,2,3},则x的值为( )
| A、3 | B、2 | C、1 | D、0 |
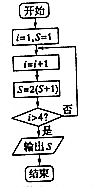 在如图所示的程序框图表示的算法中,输出的结果是
在如图所示的程序框图表示的算法中,输出的结果是