题目内容
5.已知函数f(x)=2+log3x(1≤x≤9),函数g(x)=f2(x)+f(x2),求函数g(x)的值域.分析 由函数f(x)=1+log3x的定义域是(1,9],可求得g(x)的定义域,化简g(x)=f2(x)+f(x2)求值域.
解答 解:由已知函数f(x)的定义域为x∈{x|1≤x≤9},
则g(x)的定义域满足$\left\{\begin{array}{l}{1≤x≤9}\\{1≤{x}^{2}≤9}\end{array}\right.$,
所以1≤x≤3,所以g(x)的定义域为{x||1≤x≤3};
$g(x)={(2+{log_3}x)^2}+2+{log_3}{x^2}=log_3^2x+6{log_3}x+6$,
g(x)在x∈[1,3]单调递增,
则g(x)的最大值为g(x)max=g(3)=13,
g(x)的最小值为g(x)min=g(1)=6.
故g(x)的值域为[6,13].
点评 本题考查对数的运算性质、二次函数的性质.正确的求出g(x)的定义域是关键,也是本题极易出错的地方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.将曲线C按照伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$后得到的曲线方程为x'-y'+4=0,则曲线C的方程为( )
| A. | 2x+3y-4=0 | B. | 3x-2y+4=0 | C. | 2x-3y+4=0 | D. | 3x-2y+24=0 |
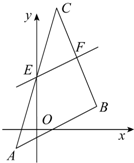 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求: