题目内容
12.已知△ABC的三个顶点在以O为球心的球面上,且 cosA=$\frac{{2\sqrt{2}}}{3}$,BC=1,AC=3,且球O的表面积为16π,则三棱锥O-ABC的体积为( )| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{14}}}{6}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
分析 由正弦定理得sinB=1,B=90°.斜边AC的中点就是△ABC的外接圆的圆心,求出三棱锥O-ABC的高h=$\sqrt{{R}^{2}-(\frac{AC}{2})^{2}}$,由此能求出三棱锥O-ABC的体积.
解答 解:△ABC的三个顶点在以O为球心的球面上,
且 cosA=$\frac{{2\sqrt{2}}}{3}$,BC=1,AC=3,
∴sin2A=1-cos2A=$\frac{1}{9}$,sinA=$\frac{1}{3}$,
由正弦定理可知:$\frac{BC}{sinA}=\frac{AC}{sinB}$,
∴sinB=1,B=90°.斜边AC的中点就是△ABC的外接圆的圆心,
∵球O的表面积为16π,∴球半径R=2,
又AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=2$\sqrt{2}$,
三棱锥O-ABC的高h=$\sqrt{{R}^{2}-(\frac{AC}{2})^{2}}$=$\sqrt{4-\frac{9}{4}}$=$\frac{\sqrt{7}}{2}$,
∴三棱锥O-ABC的体积:
V=$\frac{1}{3}×{S}_{△ABC}×h$=$\frac{1}{3}×AB×BC×h$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×1×\frac{\sqrt{7}}{2}$=$\frac{\sqrt{14}}{6}$.
故选:B.
点评 本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意正弦定理、球的性质的合理运用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
20.在△ABC中,若$\overrightarrow{AB}•(\overrightarrow{CA}+\overrightarrow{CB})=0$,且$\overrightarrow{BA}•\overrightarrow{BC}={\overrightarrow{BC}^2}$,则$\overrightarrow{AB}与\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
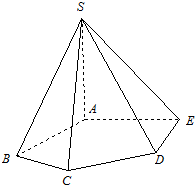 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°