题目内容
4.袋中装有大小相同,颜色不同的10张卡片,其中红色卡片5张,白色卡片3张,蓝色卡片2张,现从中随机抽取一张卡片,确定颜色后再放回袋中,若取出的是白色卡片,则不再抽取,否则,继续抽取卡片,但最多抽取3次.(Ⅰ)记“恰好取到2次红色卡片”为事件A,求P(A);
(Ⅱ)将抽取卡片的次数记为ξ,求随机变量ξ的概率分布列及数学期望E(ξ).
分析 (I)分类讨论,①前两次都取红色卡片,②第一次取红色卡片,第二次取蓝色卡片,第三次取红色卡片.③第一次取蓝色卡片,第二次取红色卡片,第三次取红色卡片.利用古典概率计算公式即可得出.
(II)ξ的取值为1,2,3.,第一次取白色卡片即可停止;第一次取蓝色或红色卡片,第二次取白色卡片.第一次与第二次取红色或蓝色卡片,第三次无论取什么卡片都停止.利用古典概率计算公式与相互对立事件的概率计算公式即可得出.
解答 解:(I)P(A)=$\frac{5×5}{10×10}$+$\frac{5×2×5}{1{0}^{3}}$+$\frac{2×5×5}{1{0}^{3}}$=$\frac{7}{20}$.
(II)ξ的取值为1,2,3.
则P(ξ=1)=$\frac{3}{10}$,P(ξ=2)=$\frac{7×3}{1{0}^{2}}$=$\frac{21}{100}$,P(ξ=3)=1-P(ξ=1)-P(ξ=2)=$\frac{49}{100}$.
∴Eξ=1×$\frac{3}{10}$+2×$\frac{21}{100}$+3×$\frac{49}{100}$=$\frac{219}{100}$=2.19.
点评 本题考查了古典概率的概率计算公式及其相互对立事件的概率计算公式及其随机变量的数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.等比数列{an}的首项为2,项数为奇数,其奇数项之和为$\frac{85}{32}$,偶数项之和为$\frac{21}{16}$,这个等比数列前n项的积为Tn(n≥2),则Tn的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,若$\sqrt{3}$(acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为$\sqrt{3}$,则此时△ABC的形状为( )
| A. | 锐角三角形 | B. | 直线三角形 | C. | 等腰三角形 | D. | 正三角形 |
9.积分$\int_0^1{{e^x}dx}$的值为( )
| A. | e | B. | e-1 | C. | 1 | D. | e2 |
12.已知△ABC的三个顶点在以O为球心的球面上,且 cosA=$\frac{{2\sqrt{2}}}{3}$,BC=1,AC=3,且球O的表面积为16π,则三棱锥O-ABC的体积为( )
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{14}}}{6}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |

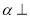 平面
平面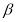 ,平面
,平面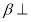 平面
平面 ,则平面
,则平面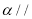 平面
平面