题目内容
给出下列六个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若|
|=|
|，则
=
；
③若
=
，则四边形ABCD是平行四边形；
④平行四边形ABCD中，一定有
=
；
⑤若
=
，
=
，则
=
；
⑥
∥
，
∥
，则
∥
．
其中不正确的命题的个数为（ ）
①两个向量相等，则它们的起点相同，终点相同；
②若|
| a |
| b |
| a |
| b |
③若
| AB |
| DC |
④平行四边形ABCD中，一定有
| AB |
| DC |
⑤若
| m |
| n |
| n |
| k |
| m |
| k |
⑥
| a |
| b |
| b |
| c |
| a |
| c |
其中不正确的命题的个数为（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：①利用向量相等即可判断出；
②若|
|=|
|，则
=
不一定成立；
③利用向量相等与平行四边形的定义即可得出；
④利用平行四边形的性质与向量相等即可得出；
⑤利用向量相等的定义即可判断出；
⑥
∥
，
∥
，则
∥
，取
=
时，
与
不一定共线．
②若|
| a |
| b |
| a |
| b |
③利用向量相等与平行四边形的定义即可得出；
④利用平行四边形的性质与向量相等即可得出；
⑤利用向量相等的定义即可判断出；
⑥
| a |
| b |
| b |
| c |
| a |
| c |
| b |
| 0 |
| a |
| c |
解答：
解：①两个向量相等，则它们的起点相同，终点相同，不一定正确；
②若|
|=|
|，方向不同，故
=
不一定成立；
③若
=
，则四边形ABCD是平行四边形，正确；
④平行四边形ABCD中，一定有
=
，正确；
⑤若
=
，
=
，则
=
，正确；
⑥
∥
，
∥
，则
∥
，取
=
时，
与
不一定共线．
其中不正确的命题的个数为1．
故选：？．
②若|
| a |
| b |
| a |
| b |
③若
| AB |
| DC |
④平行四边形ABCD中，一定有
| AB |
| DC |
⑤若
| m |
| n |
| n |
| k |
| m |
| k |
⑥
| a |
| b |
| b |
| c |
| a |
| c |
| b |
| 0 |
| a |
| c |
其中不正确的命题的个数为1．
故选：？．
点评：本题考查了向量相等的意义、向量共线定理，属于基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知x＞1，则函数f（x）=x+1+
的最小值为（ ）
| 1 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
下列选项中，p是q的必要不充分条件的是（ ）
| A、p：a+c＞b+dq：a＞b且c＞d | ||
| B、p：x=1q：x=x2 | ||
| C、p：a+bi（a，b∈R）是纯虚数q：a=0 | ||
D、p：f（x）=x3+2x2+mx+1在R上单调递增q：m≥
|
下列式子不正确的是（ ）
| A、（sin2x）′=2cos2x | ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
| ||||||||
E、
对于D，利用商的求导法则，正确． 故选B． |
已知一个角α终边上的一点坐标为（200，200），则cosα=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
下列四个函数中，在（0，+∞）上为增函数的是（ ）
| A、f（x）=3-x | ||
| B、f（x）=x2-3 | ||
C、f（x）=
| ||
| D、f（x）=-x2 |
两条异面直线指的是（ ）
| A、不同在某个平面内的两条直线 |
| B、分别在某两个平面内的两条直线 |
| C、既不平行又不相交的两条直线 |
| D、平面内的一条直线和平面外的一条直线 |
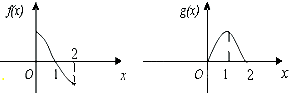已知偶函数f（x）与奇函数g（x）的定义域都是（-2，2），它们在[0，2]上的图象如图所示，则使关于x的不等式f（x）•g（x）＞0成立的x的取值范围为（ ）| A、（-2，-1）∪（1，2） |
| B、（-1，0）∪（0，1） |
| C、（-2，-1）∪（0，1） |
| D、（-1，0）∪（1，2） |