题目内容
已知x，y满足约束条件
当目标函数z＝ax＋by(a>0，b>0)在该约束条件下取到最小值2
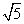时，a2＋b2的最小值为( )
A．5 B．4 C.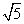 D．2
B
解析 方法一 
线性约束条件所表示的可行域如图所示．
所以z＝ax＋by在A(2,1)处取得最小值，故2a＋b＝2，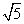
a2＋b2＝a2＋(2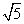－2a)2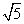＝(a－4)2＋4≥4.
方法二 画出满足约束条件的可行域知，
当目标函数过直线x－y－1＝0与2x－y－3＝0的交点(2,1)时取得最小值，
所以有2a＋b＝2.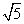
又因为a2＋b2是原点(0,0)到点(a，b)的距离的平方，
所以a2＋b2的最小值是4.故选B.
练习册系列答案
相关题目
中，
则
( ) 
B．
C．
D．
则p，q的大小关系是( )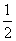
<2x<8，x∈R}，B＝{x|－1<x<m＋1，x∈R}，若x∈B成立的一个充分不必要的条件是x∈A，则实数m的取值范围是________．
B．－
C.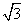
cos ωx)，其中0<ω<2.函数f(x)＝a·b－
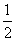，其图象的一条对称轴为x＝
.
＝1，b＝1，S△ABC＝
，若
下列结论中正确的是（ ）
B．
D．
时，
；
；
的定义域是
；
，
，则
.