题目内容
已知向量a＝(cos ωx，sin ωx)，b＝(cos ωx，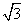
cos ωx)，其中0<ω<2.函数f(x)＝a·b－
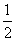，其图象的一条对称轴为x＝
.
(1)求函数f(x)的表达式及单调递增区间；
(2)在△ABC中，a，b，c分别为角A，B，C的对边，S为其面积，若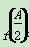
＝1，b＝1，S△ABC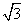＝，求a的值．
解 (1)f(x)＝a·b－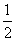
＝cos2ωx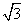＋sin ωxcos ωx－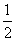
＝
＋
sin 2ωx－
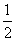
由S△ABC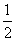＝bcsin A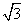＝，b＝1，得c＝4.
由余弦定理得a2＝42＋12－2×4×1×cos 
＝13，
故a＝
.
练习册系列答案
相关题目
为两个向量
间距离，若
，②
，③对任意实数t，恒有
，则( )
B．
C．
D．
，直线x＝m与f(x)，g(x)的图象分别交于M、N两点，则|MN|的最大值为________．
当目标函数z＝ax＋by(a>0，b>0)在该约束条件下取到最小值2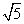
时，a2＋b2的最小值为( )
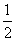)x－1，若在区间(－2,6]内关于x的方程f(x)－loga(x＋2)＝0(a>1)恰有3个不同的实数根，则a的取值范围是________．
，则满足
的集合
的个数是 个.
的值是
.