题目内容
已知等差数列{an}的公差d不为0,且a1,a3,a7成等比数列,则
的值为 .
| a1 |
| d |
考点:等比数列的性质,等差数列的性质
专题:计算题,等差数列与等比数列
分析:由等差数列{an}的公差d不为0,且a1,a3,a7成等比数列,可得(a1+2d)2=a1(a1+6d),利用d≠0,可得a1=2d,即可求出
的值.
| a1 |
| d |
解答:
解:∵等差数列{an}的公差d不为0,且a1,a3,a7成等比数列,
∴(a1+2d)2=a1(a1+6d),
∵d≠0,
∴a1=2d,
∴
=2,
故答案为:2.
∴(a1+2d)2=a1(a1+6d),
∵d≠0,
∴a1=2d,
∴
| a1 |
| d |
故答案为:2.
点评:本题考查等差数列的通项,考查等比数列的性质,比较基础.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知双曲线
-y2=1(a>0)的左焦点与抛物线y2=-12x的焦点重合,则此双曲线的渐近线方程是( )
| x2 |
| a2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±2
| ||||
D、y=±
|
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
空间直线a、b、c,平面α,则下列命题中真命题的是( ):
| A、若a⊥b,c⊥b,则a∥c |
| B、若a∥c,c⊥b,则b⊥a |
| C、若a与b是异面直线,a与c是异面直线,则b与c也是异面直线. |
| D、若a∥α,b∥α,则a∥b |
已知a=1.270.2,b=log0.3(tan46°),c=2sin29°,则a,b,c的大小关系是( )
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、a>c>b |
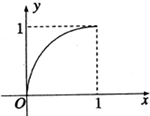 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: