题目内容
已知函数f(x)=|x-a|,g(x)=2x2+3ax+1,其中a>0.
(1)若f(x)在x≥1上是单调函数,求a的取值范围;
(2)若f(0)=g(0),求函数h(x)=f(x)+g(x),x≥1的值域.
(1)若f(x)在x≥1上是单调函数,求a的取值范围;
(2)若f(0)=g(0),求函数h(x)=f(x)+g(x),x≥1的值域.
考点:函数单调性的判断与证明,函数的值域
专题:计算题,函数的性质及应用
分析:(1)由绝对值函数的对称轴,可得f(x)在x≥a上递增,即可判断f(x)在x≥1上为增函数,即可得到a的范围;
(2)由f(0)=g(0)可得a=1,进而得到函数h(x)的解析式,运用二次函数的值域,即可得到所求值域.
(2)由f(0)=g(0)可得a=1,进而得到函数h(x)的解析式,运用二次函数的值域,即可得到所求值域.
解答:
解:(1)函数f(x)=|x-a|的对称轴为x=a,
f(x)在x≥a上递增,
则由题意可得,f(x)在x≥1上是单调函数,且为增函数,
则有a≤1,
即a的取值范围为(-∞,1];
(2)f(0)=g(0),即为|a|=1,解得a=1(-1舍去),
函数h(x)=f(x)+g(x)=|x-1|+2x2+3x+1,
由于x≥1,则h(x)=x-1+2x2+3x+1=2x2+4x
=2(x+1)2-2,
则在x≥1上递增,则h(x)≥6,
即有函数的值域为[6,+∞).
f(x)在x≥a上递增,
则由题意可得,f(x)在x≥1上是单调函数,且为增函数,
则有a≤1,
即a的取值范围为(-∞,1];
(2)f(0)=g(0),即为|a|=1,解得a=1(-1舍去),
函数h(x)=f(x)+g(x)=|x-1|+2x2+3x+1,
由于x≥1,则h(x)=x-1+2x2+3x+1=2x2+4x
=2(x+1)2-2,
则在x≥1上递增,则h(x)≥6,
即有函数的值域为[6,+∞).
点评:本题考查函数的单调性的运用,考查二次函数的值域,考查绝对值函数的单调性的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
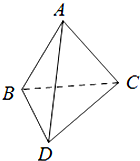 如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )
如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )