题目内容
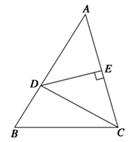
如图,在△ABC中,B=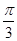 ,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
(1)若△BCD的面积为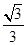 ,求CD的长;
,求CD的长;
(2)若ED=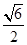 ,求角A的大小.
,求角A的大小.
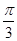 ,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
(1)若△BCD的面积为
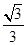 ,求CD的长;
,求CD的长;(2)若ED=
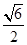 ,求角A的大小.
,求角A的大小.(1) (2)
(2)
 (2)
(2)
(1)由已知得S△BCD= BC·BD·sin B=
BC·BD·sin B=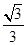 ,又BC=2,sin B=
,又BC=2,sin B= ,∴BD=
,∴BD= ,cos B=
,cos B= .
.
在△BCD中,由余弦定理,得
CD2=BC2+BD2-2BC·BD·cos B=22+ 2-2×2×
2-2×2× ×
× =
= . ∴CD=
. ∴CD= .
.
(2)∵CD=AD= ,在△BCD中,由正弦定理,得
,在△BCD中,由正弦定理,得 ,又∠BDC=2A,得
,又∠BDC=2A,得 ,解得cos A=
,解得cos A= ,所以A=
,所以A=
 BC·BD·sin B=
BC·BD·sin B=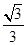 ,又BC=2,sin B=
,又BC=2,sin B= ,∴BD=
,∴BD= ,cos B=
,cos B= .
.在△BCD中,由余弦定理,得
CD2=BC2+BD2-2BC·BD·cos B=22+
 2-2×2×
2-2×2× ×
× =
= . ∴CD=
. ∴CD= .
.(2)∵CD=AD=
 ,在△BCD中,由正弦定理,得
,在△BCD中,由正弦定理,得 ,又∠BDC=2A,得
,又∠BDC=2A,得 ,解得cos A=
,解得cos A= ,所以A=
,所以A=

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
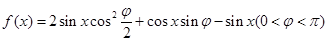 在
在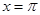 处取最小值.
处取最小值.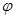 的值。
的值。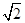 ,
,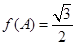 ,求角C.
,求角C. ,
, ,
,
 的最小正周期;
的最小正周期; 中,角A,B,C的对边分别为a,b,c,且满足
中,角A,B,C的对边分别为a,b,c,且满足 ,若
,若 ,求角
,求角 的值.
的值. ,
,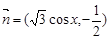 ,函数
,函数 .
. 的最大值,并求取最大值时
的最大值,并求取最大值时 的取值集合;
的取值集合;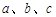 分别为
分别为 内角
内角 的对边,且
的对边,且 为锐角,且
为锐角,且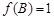 ,求
,求 的值.
的值.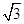 ,则c= ( ).
,则c= ( ).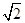




 ,
, )
) 中,
中, ,
, ,
, ,则
,则 的值为______________.
的值为______________.