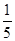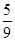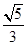题目内容
己知函数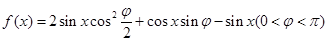 在
在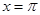 处取最小值.
处取最小值.
(1)求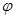 的值。
的值。
(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b=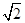 ,
,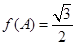 ,求角C.
,求角C.
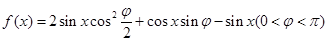 在
在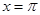 处取最小值.
处取最小值.(1)求
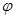 的值。
的值。(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b=
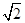 ,
,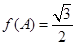 ,求角C.
,求角C.(1)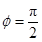 (2)
(2)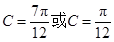
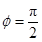 (2)
(2)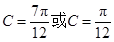
试题分析:(1)现将函数解析式化为形如
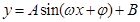 ,这时要用倍角公式、降幂公式、两角和正弦公式,即
,这时要用倍角公式、降幂公式、两角和正弦公式,即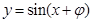 ,再利用
,再利用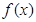 在
在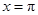 处取得最小值得关于
处取得最小值得关于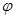 的关系式
的关系式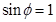 ,结合限制条件
,结合限制条件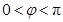 ,解出
,解出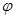 ,(2)解三角形问题,主要利用正余弦定理,本题可由
,(2)解三角形问题,主要利用正余弦定理,本题可由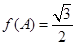 ,解出角
,解出角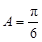 ,由正弦定理得
,由正弦定理得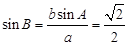 ,解出角
,解出角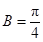 或
或 ,再由三角形内角和为
,再由三角形内角和为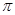 ,解出
,解出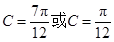 ,本题再解角
,本题再解角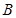 ,需注意解得个数,因为正弦函数在
,需注意解得个数,因为正弦函数在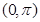 上有增有减.
上有增有减.试题解析:(1)
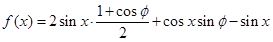
=
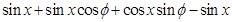 =
= 3分
3分因为
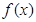 在
在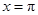 处取得最小值,所以
处取得最小值,所以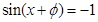 ,故
,故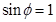 ,
,又
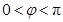 所以
所以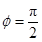 6分
6分(2)由(1)知
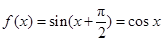 ,因为
,因为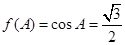 ,且A为△
,且A为△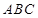 内角,所以
内角,所以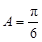 由正弦定理得
由正弦定理得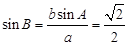 ,所以
,所以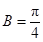 或
或 . 9分
. 9分当
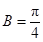 时
时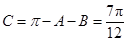 ,当
,当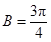 时
时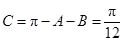 .
.综上,
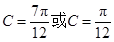 12分
12分
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
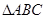 中,角
中,角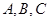 的对边分别为
的对边分别为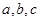 且
且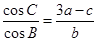 .
.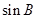 ;
; ,求
,求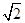 ,点M在线段PQ上.
,点M在线段PQ上.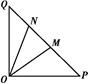
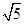 ,求PM的长;
,求PM的长; b,sin B=sin C,则B等于________.
b,sin B=sin C,则B等于________.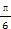 ,AC=1,AB=
,AC=1,AB=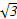 ,则BC的长为 .
,则BC的长为 .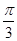 ,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.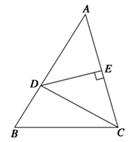
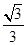 ,求CD的长;
,求CD的长;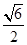 ,求角A的大小.
,求角A的大小.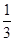 ,则sinB等于( )
,则sinB等于( )