题目内容
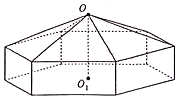 一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.
一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.考点:组合几何体的面积、体积问题,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:通过几何体的高求出棱锥的高,然后求出正六棱柱的底面边长,即可求解帐篷的体积
解答:
解:帐篷的顶点O到底面中心O1的距离为2m,帐篷的下部形状是高为1m的正六棱柱,
上部的形状是正六棱锥的高为1,侧棱长为3m的,正六棱锥的底面边长为:
=2
帐篷的体积为:V正六棱柱+V正六棱锥=6×
×(2
)2×1+
×6×
×(2
)2×1=16
.
帐篷的体积:16
.
上部的形状是正六棱锥的高为1,侧棱长为3m的,正六棱锥的底面边长为:
| 32-12 |
| 2 |
帐篷的体积为:V正六棱柱+V正六棱锥=6×
| ||
| 4 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| 2 |
| 3 |
帐篷的体积:16
| 3 |
点评:本小题主要考查组合体的体积的求法,考查运用数学知识解决实际问题的能力.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
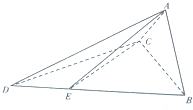 如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE= 如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证:
如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证: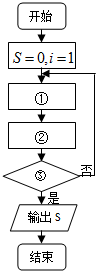 画出一个计算1+
画出一个计算1+