题目内容
4.已知F为双曲线$C:\frac{x^2}{9}-\frac{y^2}{16}=1$的左焦点,P,Q为C右支上的点,若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PFQ的周长为( )| A. | 28 | B. | 36 | C. | 44 | D. | 48 |
分析 根据题意画出双曲线图象,然后根据双曲线的定义“到两定点的距离之差为定值2a“解决.求出周长即可.
解答 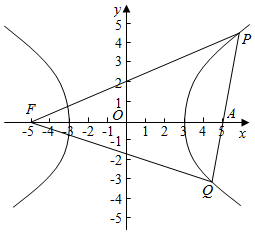 解:∵双曲线C:$\frac{x^2}{9}-\frac{y^2}{16}=1$的左焦点F(-5,0),
解:∵双曲线C:$\frac{x^2}{9}-\frac{y^2}{16}=1$的左焦点F(-5,0),
∴点A(5,0)是双曲线的右焦点,
则b=4,即虚轴长为2b=8;
双曲线图象如图:
∵|PF|-|AP|=2a=6 ①
|QF|-|QA|=2a=6 ②
而|PQ|=16,
∴①+②得:|PF|+|QF|-|PQ|=12,
∴周长为l=|PF|+|QF|+|PQ|=12+2|PQ|=44,
故选:C.
点评 本题考查三角形周长的计算,根据双曲线的定义将三角形的两边之差转化为2a,通过对定义的考查求出周长是解决本题的关键.考查学生的转化能能力.

练习册系列答案
相关题目
7. 如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
 如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
5.知函数f(x)=ex-ax的图象在区间(-1,+∞)内与x轴没有交点,则实数a的取值范围是( )
| A. | [-$\frac{1}{e}$,e) | B. | (-$\frac{1}{e}$,e) | C. | (-$\frac{1}{e}$,$\frac{1}{e}$) | D. | (0,e) |
12.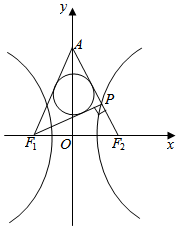 如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
 如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )
如图,F1,F2为双曲线C的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=log3(x+1),若f(a2-1)<1,则实数a的取值范围是( )
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | (-1,1) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-1)∪(1,+∞) |
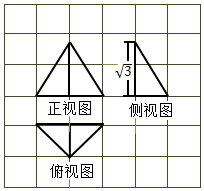 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.