已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1.x＞0}\\{-ax+1.x≤0}\end{array}\right.$.若f=0.则实数a的值等于( )A．-1B．-2C．1D．2 题目和参考答案——青夏教育精英家教网—

题目内容

20．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，x＞0}\\{-ax+1，x≤0}\end{array}\right.$，若f（a）+f（2）=0，则实数a的值等于（　　）

A．

-1

B．

-2

C．

D．

分析由f（a）+f（2）=0，得f（a）=-3，从分段函数里找到a，满足f（a）=-3即可，需分类讨论．

解答解：∵f（2）=4-1=3，
∴f（a）=-3，
∵2^x-1＞-1，
∴只有-ax+1=-3，
∴a≤0且-a²+1=-3，
∴a=-2，
故选：B．

点评本题考查分段函数找a，需分类讨论．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

10．已知离散型随机变量ξ的概率分布为

ξ	0	1	2	3
P	0.12	0.24		0.12

则P（ξ=2）=0.52．

11．

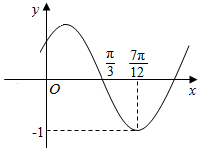函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为（　　）

A．

y=sin2x

B．

y=sin（2x+$\frac{π}{3}$）

C．

y=sin（2x+$\frac{π}{6}$）

D．

y=sin（2x-$\frac{π}{3}$）

8．下列随机试验的结果能否用离散型随机变量表示？若能，则写出各随机变量可能的取值，并说明这些值所表示的随机试验的结果．
（1）从学校回家要经过5个红绿灯口，可能遇到红灯的次数；
（2）在优、良、中、及格、不及格5个等级的测试中，某同学可能取得的成绩．

15．已知定义域为（1，+∞）的函数f（x）的导函数为f′（x），且f（e）=2，$\frac{f（x）}{x}$=lnx•f′（x），则不等式xf（x）＜2e的解集为（1，e）．

5．知函数f（x）=e^x-ax的图象在区间（-1，+∞）内与x轴没有交点，则实数a的取值范围是（　　）

（-$\frac{1}{e}$，$\frac{1}{e}$）

D．

（0，e）

12．

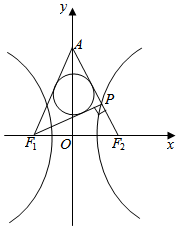如图，F₁，F₂为双曲线C的左右焦点，且|F₁F₂|=2．若双曲线C的右支上存在点P，使得PF₁⊥PF₂．设直线PF₂与y轴交于点A，且△APF₁的内切圆半径为$\frac{1}{2}$，则双曲线C的离心率为（　　）

16．设等差数列{a_n}的前n项和为S_n，且2a₅-S₄=2，3a₂+a₆=32．
（I）求数列{a_n}的通项公式；
（Ⅱ）记${T_n}=\frac{a_1}{2}+\frac{a_2}{4}+…+\frac{a_n}{2^n}，n∈{N_+}$，求T_n．

17．边长为2的正方形ABCD的顶点都在同一球面上，球心到平面ABCD的距离为1，则此球的表面积为（　　）

试题分类