题目内容
16.设{an}的相邻两项an、an+1是方程x2-cnx+($\frac{1}{3}$)n=0的两根,且a1=2,求无穷数列{cn}的各项之和.分析 通过韦达定理可知an•an+1=$\frac{1}{{3}^{n}}$,并与an+1•an+2=$\frac{1}{{3}^{n+1}}$作商可知数列{a2n-1}、{a2n}是首项分别为2、$\frac{1}{6}$,公比均为$\frac{1}{3}$的等比数列,进而分别计算出$\underset{lim}{n→∞}$(a1+a2)+(a2+a3)+(a3+a4)+…+(a2n-1+a2n)与$\underset{lim}{n→∞}$(a1+a2)+(a2+a3)+(a3+a4)+…+(a2n-1+a2n)+(a2n+a2n+1)的值即得结论.
解答 解:依题意,由韦达定理可知:an+an+1=cn,an•an+1=$\frac{1}{{3}^{n}}$,
又∵an+1•an+2=$\frac{1}{{3}^{n+1}}$,
∴$\frac{{a}_{n+2}}{{a}_{n}}$=$\frac{{a}_{n+1}•{a}_{n+2}}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{3}$,
又∵a1=2,a2=$\frac{1}{3{a}_{1}}$=$\frac{1}{6}$,
∴数列{a2n-1}、{a2n}是首项分别为2、$\frac{1}{6}$,公比均为$\frac{1}{3}$的等比数列,
又∵$\underset{lim}{n→∞}$an=0,
∴$\underset{lim}{n→∞}$(a1+a2)+(a2+a3)+(a3+a4)+…+(a2n-1+a2n)
=2$\underset{lim}{n→∞}$(a1+a3+a5+…+a2n-1)+2$\underset{lim}{n→∞}$(a2+a4+a6+…+a2n)-$\underset{lim}{n→∞}$(a2n+a1)
=2$\underset{lim}{n→∞}$$\frac{2(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$+2$\underset{lim}{n→∞}$$\frac{\frac{1}{6}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-$\underset{lim}{n→∞}$(a2n+2)
=2$\underset{lim}{n→∞}$3(1-$\frac{1}{{3}^{n}}$)+2$\underset{lim}{n→∞}$$\frac{1}{4}$(1-$\frac{1}{{3}^{n}}$)-$\underset{lim}{n→∞}$(a2n+2)
=6+$\frac{1}{2}$-2
=$\frac{9}{2}$,
同理可得$\underset{lim}{n→∞}$(a1+a2)+(a2+a3)+(a3+a4)+…+(a2n-1+a2n)+(a2n+a2n+1)=$\frac{9}{2}$,
综上所述,所求值为$\frac{9}{2}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 学习实践园地系列答案
学习实践园地系列答案 如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )
如图,某电路在A、B之间有四个焊接点,现已知一个焊点脱落导致电路不通,则焊点脱落的不同情况有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
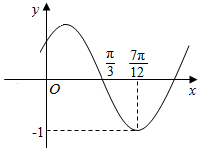 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向右平移$\frac{π}{6}$个单位后得到的函数图象的解析式为( )| A. | y=sin2x | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin(2x-$\frac{π}{3}$) |
| A. | [-$\frac{1}{e}$,e) | B. | (-$\frac{1}{e}$,e) | C. | (-$\frac{1}{e}$,$\frac{1}{e}$) | D. | (0,e) |
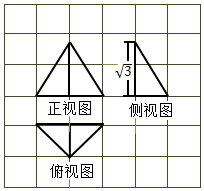 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.