题目内容
2．在△ABC中，角A，B，C所对的边分别为a，b，c，若$\sqrt{3}acosB+bsinA=0$，则B=（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
分析 根据条件和正弦定理得出tanB，得出B．
解答 解：在△ABC中，∵$\sqrt{3}acosB+bsinA=0$，∴$\frac{a}{sinA}=\frac{b}{-\sqrt{3}cosB}$，
又∵$\frac{a}{sinA}=\frac{b}{sinB}$，
∴sinB=-$\sqrt{3}$cosB，
∴tanB=-$\sqrt{3}$．
∴B=$\frac{2π}{3}$．
故选：C．
点评 本题考查了正弦定理，特殊角的三角函数值，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
12．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤0}\\{{-x}^{2}，x＞0}\end{array}\right.$，不等式f（ax2）+f（1-ax）＜0对任意的x∈R都成立，则实数a的取值范围（ ）
| A． | （0，4） | B． | （-4，0） | C． | [0，4） | D． | [0，4] |
13．复数$\frac{3-i}{i}$=（ ）
| A． | 1+3i | B． | -1-3i | C． | -1+3i | D． | 1-3i |
10．
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目．以普通人讲述手中账单背后的故事，并参与因此而量身为其定制的大型游戏，来赢得账单报销的形式，讲述了人与人之间的真情，展现了当今百姓生活中的万般幸福之态．某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究，由此得到如下频数分布表：
（Ⅰ）在如表中作出这些数据的频率分布直方图：
（Ⅱ）若将频率视为概率，从参与节目的报账人中随机抽取3位（看作有放回的抽样），求账单总额在[3000，4000）内的报账人数X的分布列、数学期望、与方差．
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目．以普通人讲述手中账单背后的故事，并参与因此而量身为其定制的大型游戏，来赢得账单报销的形式，讲述了人与人之间的真情，展现了当今百姓生活中的万般幸福之态．某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究，由此得到如下频数分布表：| 报账人的账单总额（元） | [0，1000） | [1000，2000） | [2000，3000） | [3000，4000） | [4000，5000） | [5000，6000） |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
（Ⅱ）若将频率视为概率，从参与节目的报账人中随机抽取3位（看作有放回的抽样），求账单总额在[3000，4000）内的报账人数X的分布列、数学期望、与方差．
17．某工厂一年中各月份的收入、支出情况的统计如图所示，下列说法中错误的是（ ）
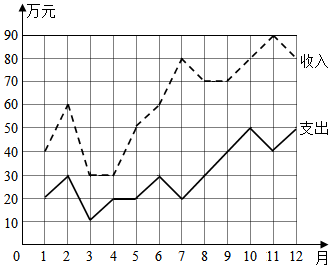
（注：结余=收入-支出）
（注：结余=收入-支出）
| A． | 收入最高值与收入最低值的比是3：1 | |
| B． | 结余最高的月份是7月 | |
| C． | 1至2月份的收入的变化率与4至5月份的收入的变化率相同 | |
| D． | 前6个月的平均收入为40万元 |