题目内容
15.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象与x轴的一个交点$(-\frac{π}{12},0)$到其相邻的一条对称轴的距离为$\frac{π}{4}$.若$f(\frac{π}{12})=\frac{3}{2}$,则函数f(x)在$[0,\frac{π}{2}]$上的最小值为( )| A. | $\frac{1}{2}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
分析 由题意可求函数的周期T,利用周期公式可求ω的值,由Asin[2×$(-\frac{π}{12})$+φ]=0,结合范围0<φ<π,可得φ,由$f(\frac{π}{12})=\frac{3}{2}$,可解得A的值,由x∈$[0,\frac{π}{2}]$,可得2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],利用正弦函数的图象和性质即可求解.
解答 解:∵由题意,函数的周期T=4×$\frac{π}{4}$=π=$\frac{2π}{ω}$,解得:ω=2.
∵点$(-\frac{π}{12},0)$在函数图象上,可得:Asin[2×$(-\frac{π}{12})$+φ]=0,解得:φ=kπ+$\frac{π}{6}$,k∈Z,
∴由0<φ<π,可得:φ=$\frac{π}{6}$.
∵$f(\frac{π}{12})=\frac{3}{2}$,可得:Asin(2×$\frac{π}{12}$+$\frac{π}{6}$)=$\frac{3}{2}$,
∴解得:A=$\sqrt{3}$,
∴f(x)=$\sqrt{3}$sin(2x+$\frac{π}{6}$).
∵x∈$[0,\frac{π}{2}]$,
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴当2x+$\frac{π}{6}$=$\frac{7π}{6}$,即x=$\frac{π}{2}$时,函数f(x)在$[0,\frac{π}{2}]$上的最小值为-$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题主要考查了三角函数的周期性及其求法,正弦函数的图象和性质,考查了转化思想和数形结合思想,属于中档题.

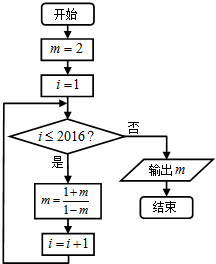
| A. | -3 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | b<a<c |
 某校某年级有100名学生,已知这些学生完成家庭作业的时间均在区间[0.5,3.5)内(单位:小时),现将这100人完成家庭作业的时间分为3组:[0.5,1.5),[1.5,2.5),[2.5,3.5)加以统计,得到如图所示的频率分布直方图.在这100人中,采用分层抽样的方法抽取10名学生研究其视力状况与完成作业时间的相关性,则在抽取样本中,完成作业的时间超过1.5个小时的有5人.
某校某年级有100名学生,已知这些学生完成家庭作业的时间均在区间[0.5,3.5)内(单位:小时),现将这100人完成家庭作业的时间分为3组:[0.5,1.5),[1.5,2.5),[2.5,3.5)加以统计,得到如图所示的频率分布直方图.在这100人中,采用分层抽样的方法抽取10名学生研究其视力状况与完成作业时间的相关性,则在抽取样本中,完成作业的时间超过1.5个小时的有5人.