题目内容
1.已知命题p,q,则“¬p或q为假”是“p且¬q为真”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由“¬p或q为假”,可得¬p或q为假,即p且¬q为真.即可判断出结论.
解答 解:“¬p或q为假”,则¬p或q为假,∴p且¬q为真,
∴“¬p或q为假”是“p且¬q为真”的充要条件.
故选:C.
点评 本题考查了复合命题的直角的判定方法,考查了推理能力,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{{-x}^{2},x>0}\end{array}\right.$,不等式f(ax2)+f(1-ax)<0对任意的x∈R都成立,则实数a的取值范围( )
| A. | (0,4) | B. | (-4,0) | C. | [0,4) | D. | [0,4] |
13.复数$\frac{3-i}{i}$=( )
| A. | 1+3i | B. | -1-3i | C. | -1+3i | D. | 1-3i |
10. 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
(Ⅰ)在如表中作出这些数据的频率分布直方图:
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
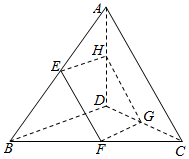 如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形.
如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形. 某校某年级有100名学生,已知这些学生完成家庭作业的时间均在区间[0.5,3.5)内(单位:小时),现将这100人完成家庭作业的时间分为3组:[0.5,1.5),[1.5,2.5),[2.5,3.5)加以统计,得到如图所示的频率分布直方图.在这100人中,采用分层抽样的方法抽取10名学生研究其视力状况与完成作业时间的相关性,则在抽取样本中,完成作业的时间超过1.5个小时的有5人.
某校某年级有100名学生,已知这些学生完成家庭作业的时间均在区间[0.5,3.5)内(单位:小时),现将这100人完成家庭作业的时间分为3组:[0.5,1.5),[1.5,2.5),[2.5,3.5)加以统计,得到如图所示的频率分布直方图.在这100人中,采用分层抽样的方法抽取10名学生研究其视力状况与完成作业时间的相关性,则在抽取样本中,完成作业的时间超过1.5个小时的有5人.