题目内容
3.若$\left\{\begin{array}{l}{x+4y-8≤0}\\{x≥0}\\{y>0}\end{array}\right.$在区域内任取一点P,则点P落在圆x2+y2=2内的概率为$\frac{π}{16}$.分析 作出不等式组对应的平面区域,求出对应区域的面积,根据几何概型的概率公式进行求解即可.
解答  解:不等式组对应的平面区域为三角形OAB,其中A(8,0),B(0,2),对应的面积为S=$\frac{1}{2}$×2×8=8,
解:不等式组对应的平面区域为三角形OAB,其中A(8,0),B(0,2),对应的面积为S=$\frac{1}{2}$×2×8=8,
x2+y2=2表示的区域为半径为$\sqrt{2}$的圆在三角形OAB内部的部分,对应的面积为$\frac{1}{4}$π•($\sqrt{2}$)2=$\frac{π}{2}$,
∴根据几何概型的概率公式,得到所求对应概率P=$\frac{\frac{π}{2}}{8}$=$\frac{π}{16}$.
故答案为:$\frac{π}{16}$.
点评 本题主要考查几何概型的概率公式,利用二元一次不等式组表示平面区域求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
14.某省每年损失耕地20万亩,每亩耕地价值24000元,为了减少耕地损失,决定按耕地价格的t%征收耕地占用税,这样每年的耕地损失可减少$\frac{5}{2}$t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
| A. | [1,3] | B. | [3,5] | C. | [5,7] | D. | [7,9] |
15.已知函数f(x)=x2-mx-m2,则f(x)( )
| A. | 有一个零点 | B. | 有两个零点 | ||
| C. | 有一个或两个零点 | D. | 无零点 |
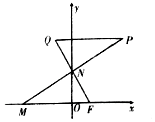 已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.
已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.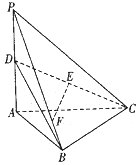 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.