题目内容
已知极坐标的极点在直角坐标系的原点O处,极轴与x轴的正半轴重合,曲线C的参数方程为
(θ为参数),直线l的极坐标方程为ρcos(θ-
)=6.点P在曲线C上,则点P到直线l的距离的最小值为 .
|
| π |
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:本题先将消去参数,将曲线C的参数方程化成普通方程,再利用公式将直线l的极坐标方程化成平面直角坐标方程,
解答:
解:∵曲线C的参数方程为
(θ为参数),
∴消去参数θ后得到:
+y2=1,
∵
,
∴直线l的极坐标方程为ρcos(θ-
)=6可转化为:
∴ρcosθcos
+ρsinθsin
=6,
∴
x+
y=6,
∴直线l的方程为:x+
y-12=0.
将直线l平移至与y轴相切,得到直线l′,设直线l′的方程为:
x+
y+m=0.
由
得:
∴12y2+2
my+m2-9=0,
令△=0,
(2
m)2-4×12(m2-9)=0,
m=±2
.
取m=-2
,
直线l′的方程为:x+
y-2
=0.
∴直线l、l′间距离为:
d=
=6-
.
故答案为:6-
.
|
∴消去参数θ后得到:
| x2 |
| 9 |
∵
|
∴直线l的极坐标方程为ρcos(θ-
| π |
| 3 |
∴ρcosθcos
| π |
| 3 |
| π |
| 3 |
∴
| 1 |
| 2 |
| ||
| 2 |
∴直线l的方程为:x+
| 3 |
将直线l平移至与y轴相切,得到直线l′,设直线l′的方程为:
x+
| 3 |
由
|
∴12y2+2
| 3 |
令△=0,
(2
| 3 |
m=±2
| 3 |
取m=-2
| 3 |
直线l′的方程为:x+
| 3 |
| 3 |
∴直线l、l′间距离为:
d=
|-12+2
| ||
|
| 3 |
故答案为:6-
| 3 |
点评:本题考查了参数方程、极坐标方程与平面直角坐标方程的转化,本题难度不大,属于基础题.

练习册系列答案
相关题目
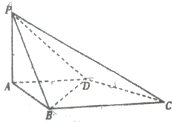 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.