Question

18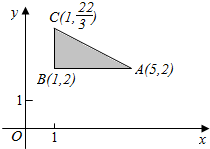．如图所示的坐标平面的可行域内（阴影部分且包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（　　）

• A． $\frac{1}{4}$
• B． $\frac{3}{5}$
• C． 4
• D． $\frac{4}{3}$

Answer 1

分析 由两点坐标求出AC所在直线斜率，化目标函数为直线方程的斜截式，由使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，得-a=-$\frac{4}{3}$，从而求得a的值．

解答 解：如图，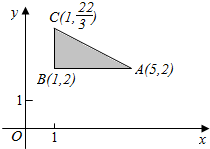

${k}_{AC}=\frac{\frac{22}{3}-2}{1-5}=-\frac{4}{3}$．
化目标函数z=ax+y（a＞0）为y=-ax+z，
要使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则-a=-$\frac{4}{3}$，即a=$\frac{4}{3}$．
故选：D．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．