题目内容
8．若扇形的弧长和半径都为2，则此扇形的面积为2．分析 根据扇形的面积=$\frac{1}{2}$×弧长×半径求出即可．
解答 解：∵扇形的弧长和半径都为2，
∴S扇形=$\frac{1}{2}$lr=$\frac{1}{2}$×2×2=2，
故答案为：2．
点评 此题考查了扇形面积的计算，主要考查了扇形面积的求算方法．面积公式有两种：
（1）利用圆心角和半径：s=$\frac{nπ{r}^{2}}{360}$；
（2）利用弧长和半径：s=$\frac{1}{2}$lr．针对具体的题型选择合适的方法．
练习册系列答案
阅读快车系列答案
相关题目
19．已知2sin2α=1+cos2α，则tan2α=（ ）
| A． | $-\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{4}{3}$或0 | D． | $-\frac{4}{3}$或0 |
16．若变量x，y满足条件$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x+y≤2}\end{array}\right.$的z=2x+y的取值范围是（ ）
| A． | [3，4] | B． | [2，4] | C． | [2，3] | D． | [0，2] |
17．边长与对角线长均相等的空间四边形ABCD中，AB与CD的中点分别是P、Q，作与直线PQ垂直的任一平面α，则空间四边形ABCD在平面α内的射影是（ ）
| A． | 梯形 | B． | 矩形但非正方形 | C． | 菱形但非正方形 | D． | 正方形 |
18．
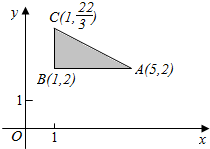如图所示的坐标平面的可行域内（阴影部分且包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）
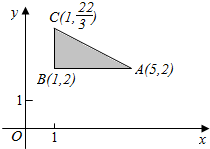如图所示的坐标平面的可行域内（阴影部分且包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{3}{5}$ | C． | 4 | D． | $\frac{4}{3}$ |