题目内容
3.若0<θ<π,且满足tan$\frac{θ}{2}$+tan$\frac{3θ}{2}$+tan$\frac{θ}{2}$tan$\frac{3θ}{2}$=1,则θ=$\frac{π}{8}$或$\frac{5π}{8}$.分析 利用两角和的正切函数,求出2θ的正切函数值,然后求解角的大小.
解答 解:θ满足tan$\frac{θ}{2}$+tan$\frac{3θ}{2}$+tan$\frac{θ}{2}$tan$\frac{3θ}{2}$=1,
可得tan$\frac{θ}{2}$+tan$\frac{3θ}{2}$=1-tan$\frac{θ}{2}$tan$\frac{3θ}{2}$,
可得tan2θ=tan($\frac{θ}{2}+\frac{3θ}{2}$)=1,
∵0<θ<π,2θ∈(0,2π),
∴2θ=$\frac{π}{4}$或$\frac{5π}{4}$,
解得θ=$\frac{π}{8}$或$\frac{5π}{8}$.
故答案为:$\frac{π}{8}$或$\frac{5π}{8}$.
点评 本题考查两角和的正切函数的应用,注意角所在范围,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.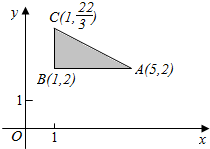 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
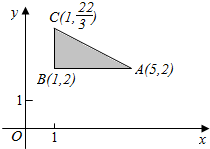 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{4}{3}$ |