题目内容
8.设函数f(x),g(x)有相同的定义域D,且f(x)为增函数,g(x)为减函数,则函数f(x)+g(x),f(x)-g(x)中哪一个为增函数?分析 容易根据已知条件得到f(x)-g(x)为增函数,而f(x)+g(x)的单调性不能判断,可根据增函数、减函数的定义证明f(x)-g(x)为增函数:设任意的x1,x2∈D,作差比较f(x1)-g(x1)与f(x2)-g(x2)的大小关系,需利用上f(x),g(x)在D上的单调性,从而证出f(x1)-g(x1)<f(x2)-g(x2),便得出f(x)-g(x)为增函数.
解答 解:f(x)-g(x)为增函数,f(x)+g(x)不一定为增函数,比如f(x)=x,g(x)=-x;
证明f(x)-g(x)为增函数:设x1,x2∈D,且x1<x2,则:
∵f(x)在D上为增函数,g(x)在D上为减函数;
∴f(x1)<f(x2),g(x1)>g(x2);
设F(x)=f(x)-g(x),则:
F(x1)-F(x2)=f(x1)-g(x1)-f(x2)+g(x2)=[f(x1)-f(x2)]+[g(x2)-g(x1)]<0;
∴F(x1)<F(x2);
∴F(x)在D上为增函数;
即f(x)-g(x)在D上为增函数.
点评 考查增函数、减函数的定义,以及根据增函数的定义证明一个函数为增函数的方法和过程,作差比较F(x1)与F(x2)大小的方法,以及增函数和减函数定义的运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
18.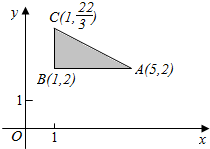 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
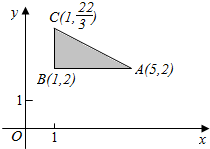 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{4}{3}$ |
16.已知函数f(x)=$\left\{\begin{array}{l}{2x+1,x≥0}\\{3x+1,x<0}\end{array}\right.$,若f(2-3a)>f(a),则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,+∞) | D. | (-∞,-$\frac{1}{2}$) |
17.数列$\frac{1}{2}$,$\frac{2}{4}$,$\frac{3}{8}$,$\frac{4}{16}$,…的前10项的和为( )
| A. | $\frac{507}{256}$ | B. | $\frac{507}{128}$ | C. | $\frac{509}{128}$ | D. | $\frac{509}{256}$ |