题目内容
已知函数f(x)＝2x2－ax＋ln x在其定义域上不单调，则实数a的取值范围是( )
A．(－∞，4] B．(－∞，4)
C．(4，＋∞) D．[4，＋∞)
C
[解析] 函数f(x)的定义域为(0，＋∞)，
因为f(x)＝2x2－ax＋ln x，所以f′(x)＝4x－a＋
＝(4x2－ax＋1)．
由函数f(x)在区间(0，＋∞)上不单调可知f′(x)＝0有两个正解，即4x2－ax＋1＝0有两个正解，设为x1，x2.
故有
解得a>4.
所以a的取值范围为(4，＋∞)．
练习册系列答案
阅读快车系列答案
相关题目
的公差为2，若
，
，
成等比数列，则
的前n项和
（ ）
B、
C、
D、
对任意实数
均有（a+b）=（a）·（b），且当
时，
．
； 
时，解不等式
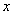的一元二次方程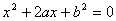
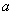是从0，1，2，3四个数中任意取一个数，
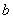是从0，1，2三个数中任意取一个，求上述方程有实根的概率
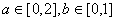，求上述方程有实根的概率
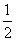anan＋1.
.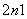