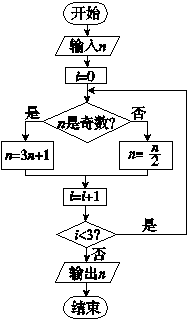
题目内容
在如图所示的数表中,第i行第j列的数记为a(i,j),且a(1,j)=2j-1,a(i,1)=i,a(i+1,j+1)=a(i,j)+a(i+1,j),则此数表中若记第3行的数3,5,8,13,22,…,为数列{bn},则{bn}的通项公式为________.

bn=2n-1+n+1
[解析] 由题意可得n≥2时,a(2,n)=2+1+2+22+…+2n-2=2+ =2n-1+1,n=1时,经验证知成立,a(2,n)=2n-1+1.则n≥2时,a(3,n)=3+(1+1)+(2+1)+(22+1)+…+(2n-2+1)=3+
=2n-1+1,n=1时,经验证知成立,a(2,n)=2n-1+1.则n≥2时,a(3,n)=3+(1+1)+(2+1)+(22+1)+…+(2n-2+1)=3+ +n-1=2n-1+n+1.n=1时,经验证成立,∴a(3,n)=2n-1+n+1,即bn=2n-1+n+1.
+n-1=2n-1+n+1.n=1时,经验证成立,∴a(3,n)=2n-1+n+1,即bn=2n-1+n+1.

练习册系列答案
相关题目

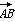 与
与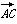 的夹角为60°,且|
的夹角为60°,且| ,则
,则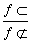 =________.
=________.
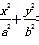 =1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )
=1(a>b>0)上一点,若PF1⊥PF2,tan ∠PF2F1=2,则椭圆的离心率e=( )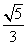 B.
B.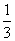 C.
C.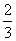 D.
D.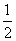
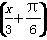 ,f(3α+π)=
,f(3α+π)= ,f
,f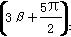 =-
=-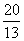 ,其中α,β∈
,其中α,β∈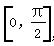 ,则cos(α-β)的值为( )
,则cos(α-β)的值为( )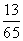 B.
B.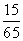 C.
C.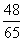 D.
D.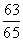
 B. 16
B. 16 C. 9
C. 9