题目内容
3.已知单位向量$\overrightarrow a$,$\overrightarrow b$,满足$\overrightarrow a⊥({\overrightarrow a+2\overrightarrow b})$,则$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 设单位向量$\overrightarrow a$,$\overrightarrow b$的夹角为θ,根据$\overrightarrow a⊥({\overrightarrow a+2\overrightarrow b})$,得$\overrightarrow{a}$•($\overrightarrow{a}$+2$\overrightarrow{b}$)=0,代入数据求出cosθ的值.
解答 解:设单位向量$\overrightarrow a$,$\overrightarrow b$的夹角为θ,
∵$\overrightarrow a⊥({\overrightarrow a+2\overrightarrow b})$,
∴$\overrightarrow{a}$•($\overrightarrow{a}$+2$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$$•\overrightarrow{b}$=0,
即12+2×1×1×cosθ=0,
解得cosθ=-$\frac{1}{2}$,
∴$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为-$\frac{1}{2}$.
故选:D.
点评 本题考查了平面向量的运算法则以及数量积和夹角的计算问题,是基础题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
11.若将函数f(x)=$\left\{\begin{array}{l}{2|x|-2,x∈[-1,1]}\\{f(x-2),x∈(1,+∞)}\end{array}\right.$的正零点从小到大依次排成一列,得到数列{an},n∈N*,则数列{(-1)n+1an}的前2017项和为( )
| A. | 4032 | B. | 2016 | C. | 4034 | D. | 2017 |
18.某商家在网上销售一种商品,从该商家的销售数据中抽取6天的价格与销量的对应数据,如下表所示:
(Ⅰ)由表中数据,看出可用线性回归模型拟合y与x的关系,试求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并预测当价格为1000元时,每天的商品的销量为多少;
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率作为客户A,B购买此商品的概率,而客户C,D购买此商品的概率均为$\frac{1}{2}$,设这4位客户中购买此商品的人数为X,求X的分布列和数学期望.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率作为客户A,B购买此商品的概率,而客户C,D购买此商品的概率均为$\frac{1}{2}$,设这4位客户中购买此商品的人数为X,求X的分布列和数学期望.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
13.已知集合A={x|0<x<2},集合B={x|-1<x<1},集合C={x|mx+1>0},若A∪B⊆C,则实数m的取值范围为( )
| A. | {m|-2≤m≤1} | B. | {m|-$\frac{1}{2}$≤m≤1} | C. | {m|-1≤m≤$\frac{1}{2}$} | D. | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
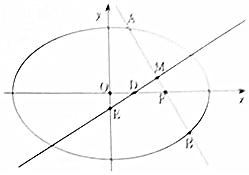 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.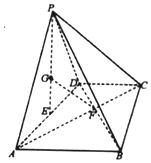 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F