题目内容
7．抛物线y=$\frac{x^2}{4}$的焦点为F，点P在抛物线上，点O为坐标原点，若|PF|=5，则|PO|等于（ ）| A． | 6 | B． | 5$\sqrt{2}$ | C． | 5 | D． | 4$\sqrt{2}$ |
分析 求出抛物线的焦点和准线方程，设出P的坐标，运用抛物线的定义，可得|PF|=d（d为P到准线的距离），求出P的坐标，即可得到所求值．
解答 解：抛物线x2=4y的焦点F（0，1），准线l为y=-1，
设抛物线的点P（m，n），
则由抛物线的定义，可得|PF|=d（d为P到准线的距离），
即有n+1=5，
解得，n=4，
∴P（±4，4），
∴|PO|=4$\sqrt{2}$．
故选：D．
点评 本题考查抛物线的定义、方程和性质，考查运算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．设定义在R上的偶函数y=f（x），满足对任意t∈R都有f（t）=f（2-t），且x∈[0，1]时，f（x）=-ln（x2+e），则f（2016）的值等于（ ）
| A． | -ln（e+1） | B． | -ln（4+e） | C． | -1 | D． | $-ln（e+\frac{1}{4}）$ |
18．某棱锥的三视图如图所示，则该几何体的体积为（ ）
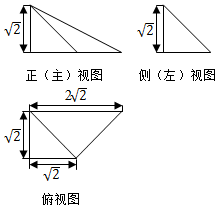
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | 3$\sqrt{2}$ |
12．设a＞b＞0，则下列不等式恒成立的为（ ）
| A． | $\frac{1}{a}$＞$\frac{1}{b}$ | B． | ac＞bc | C． | $\sqrt{a}$＞$\sqrt{b}$ | D． | $\frac{a}{c}$＞$\frac{b}{c}$ |
在四棱锥P-ABCD中，CD⊥平面PAD，AB∥CD，AD⊥PA，△ADC、△PAD均为等腰三角形，AD=4AB=4，M为线段CP上一点，且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$（0≤λ≤1）．