题目内容
17.设定义在R上的偶函数y=f(x),满足对任意t∈R都有f(t)=f(2-t),且x∈[0,1]时,f(x)=-ln(x2+e),则f(2016)的值等于( )| A. | -ln(e+1) | B. | -ln(4+e) | C. | -1 | D. | $-ln(e+\frac{1}{4})$ |
分析 由已知得f(2+t)=f(2-2-t)=f(-t)=f(t),由此利用x∈[0,1]时,f(x)=-ln(x2+e),能求出f(2016).
解答 解:∵定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(2-t),
∴f(2+t)=f(2-2-t)=f(-t)=f(t),
∵x∈[0,1]时,f(x)=-ln(x2+e),
∴f(2016)=f(1008×2)=f(0)=-lne=-1.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知函数f(x)=x+tanx+1,若f(a)=2,则f(-a)的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | 3 |
5.设A,B是椭圆$\frac{{x}^{2}}{2}$+y2=1上的两个动点,O是坐标原点,且AO⊥BO,作OP⊥AB,垂足为P,则|OP|=( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.已知向量$\vec a$,$\vec b$的夹角为120°,且$|\vec a|=2$,$|\vec b|=1$,$|{\vec a+2\vec b}|$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
9.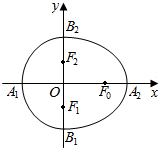 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )
 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\frac{{\sqrt{7}}}{2},1$ | C. | $1,\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2},1$ |
7.抛物线y=$\frac{x^2}{4}$的焦点为F,点P在抛物线上,点O为坐标原点,若|PF|=5,则|PO|等于( )
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |