题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则z=$\sqrt{(x-5)^{2}+(y-1)^{2}}$的最小值为( )| A. | $\frac{4}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2 |
分析 作出可行域,z表示区域内的点与(5,1)间的距离,数形结合及点到直线的距离公式可得.
解答 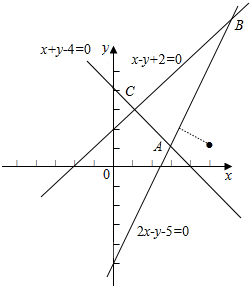 解:作出$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$所对应的可行域(如图△ABC),
解:作出$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$所对应的可行域(如图△ABC),
z=$\sqrt{(x-5)^{2}+(y-1)^{2}}$表示区域内的点与(5,1)间的距离,
结合图象可得z的最小值为(5,1)到直线2x-y-5=0的距离,
由点到直线的距离公式可得z的最小值为$\frac{|2×5-1-5|}{\sqrt{{2}^{2}+(-1)^{2}}}$=$\frac{4}{5}\sqrt{5}$,
故选:A.
点评 本题考查简单线性规划,涉及点到直线的距离公式,准确作图是解决问题的关键,属中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.在平面直角坐标系中,方程|x|+|y|=4所表示的曲线是( )
| A. | 三角形 | B. | 非正方形的长方形 | ||
| C. | 正方形 | D. | 非正方形的菱形 |
19.在复平面内,z1=1+3i,z2=-2+4i,复数z=z1+z2,则复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列有关命题的说法正确的是( )
| A. | 命题“若x=y,则x2=y2”的逆否命题为真命题 | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |