题目内容
9.给出下列结论:①函数y=2x2-1在x=3处的导数为11;
②若物体的运动规律是s=f(t),则物体在时刻t0的瞬时速度v等于f′(t0);
③物体做直线运动时,它的运动规律可以用函数v=v(t)描述,其中v表示瞬时速度,t表示时间,那么该物体运动的加速度为a=$\underset{lim}{△t→0}$$\frac{v(t+△t)-v(t)}{△t}$;
④若f(x)=$\sqrt{x}$,则f′(0)=0.
其中正确的结论序号为②③.
分析 根据导数的概念及运算法则,逐一分析四个结论的真假,可得答案.
解答 解:①函数y=2x2-1的导函数为:y′=4x,故在x=3处的导数为12,故错误;
②若物体的运动规律是s=f(t),则物体在时刻t0的瞬时速度v等于f′(t0),故正确;
③物体做直线运动时,它的运动规律可以用函数v=v(t)描述,其中v表示瞬时速度,t表示时间,那么该物体运动的加速度为该点处的导数值,即a=$\underset{lim}{△t→0}$$\frac{v(t+△t)-v(t)}{△t}$,故正确;
④若f(x)=$\sqrt{x}$,则f′(x)=$\frac{1}{2\sqrt{x}}$,则f′(0)不存在,故错误.
故正确的结论序号为:②③,
故答案为:②③.
点评 本题以命题的真假判断与应用为载体,考查了导函数的几何意义及运算法则,难度中档.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
20.用二分法求方程x2=($\frac{1}{2}$)x-2的近似解时,所取的初始区间可以是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
14.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则z=$\sqrt{(x-5)^{2}+(y-1)^{2}}$的最小值为( )
| A. | $\frac{4}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2 |
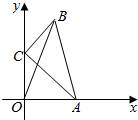 在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.
在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.