题目内容
1.已知f(cosx)=cos5x,则f(sin30°)=$\frac{1}{2}$.分析 由条件利用诱导公式可得要求的式子即 f(cos60°)=cos300°=cos60°,从而得到结果.
解答 解:f(cosx)=cos5x,则f(sin30°)=f(cos60°)=cos300°
=cos(-60°)=cos60°=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查诱导公式的应用,求函数的值,属于基础题.

练习册系列答案
相关题目
14.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则z=$\sqrt{(x-5)^{2}+(y-1)^{2}}$的最小值为( )
| A. | $\frac{4}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2 |
12.y=2x关于直线y=x对称的函数为( )
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y={({\frac{1}{2}})^x}$ | C. | y=log2x | D. | y=2-x |
6.已知向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x,3),若$\overrightarrow{a}$与$\overrightarrow{b}$共线,则|$\overrightarrow{a}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
10.执行如图所示的程序框图,若输出的n=6,则输入整数p的最小值是.( )


| A. | 17 | B. | 16 | C. | 18 | D. | 19 |
11.执行如图的程序框图,若输入a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
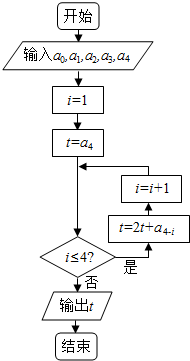

| A. | 5 | B. | 10 | C. | 12 | D. | 14 |