题目内容
2.已知sinx=$\frac{\sqrt{5}-1}{2}$,sin2($\frac{x}{2}$-$\frac{π}{4}$)的值等于$\frac{3-\sqrt{5}}{4}$.分析 根据sinx的值,用倍角公式化简sin2($\frac{x}{2}$-$\frac{π}{4}$),即可求值.
解答 解:∵sinx=$\frac{\sqrt{5}-1}{2}$,
∴sin2($\frac{x}{2}$-$\frac{π}{4}$)=$\frac{1}{2}$[1-cos(x-$\frac{π}{2}$)]
=$\frac{1}{2}$(1-sinx)
=$\frac{1}{2}$-$\frac{1}{2}$×$\frac{\sqrt{5}-1}{2}$
=$\frac{3-\sqrt{5}}{4}$.
故答案为:$\frac{3-\sqrt{5}}{4}$.
点评 本题考查了倍角公式的应用问题,也考查了三角函数求值的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则z=$\sqrt{(x-5)^{2}+(y-1)^{2}}$的最小值为( )
| A. | $\frac{4}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2 |
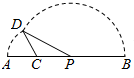 如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )
如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )