题目内容
若曲线f（x）=lnx-ax（a∈R）在点（1，f（1））处的切线与直线x-y+1=0垂直，则a= ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义结合直线垂直的等价条件，即可得到结论．
解答：
解：∵函数在点（1，f（1））处的切线与直线x-y+1=0，
∴切线斜率k=-1，即k=f′（1）=-1，
∵f（x）=lnx-ax，
∴f′（x）=
-a，
即k=f′（1）=1-a=-1，
解得a=2，
故答案为：2
∴切线斜率k=-1，即k=f′（1）=-1，
∵f（x）=lnx-ax，
∴f′（x）=
| 1 |
| x |
即k=f′（1）=1-a=-1，
解得a=2，
故答案为：2
点评：本题主要考查导数的几何意义的应用以及直线垂直的关系，根据导数求出函数的切线斜率是解决本题的关键．
练习册系列答案
相关题目
已知集合A={-1，0，1}，B={x|1≤2x＜4}，则A∩B等于（ ）
| A、{1} |
| B、{-1，1} |
| C、{1，0} |
| D、{-1，0，1} |
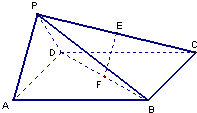如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，若E、F分别为PC、BD的中点．
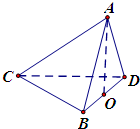如图，四面体ABCD中，O是BD的中点，CA=CB=CD=BD=2，AB=AD=直线y=kx+3与圆（x-2）2+（y-3）2=4相交于M、N两点，若|MN|≤2
，则k的取值范围是（ ）
| 3 |
A、[
| ||||||||
B、(0，
| ||||||||
C、(-∞，-
| ||||||||
D、[-
|