题目内容
已知定义域为R的函数f(x)=
是奇函数;
(1)求函数f(x)的解析式;
(2)求不等式f(x)>-
的取值集合.
| 2x-b |
| 2x+1+a |
(1)求函数f(x)的解析式;
(2)求不等式f(x)>-
| 3 |
| 10 |
考点:指、对数不等式的解法,函数解析式的求解及常用方法,函数奇偶性的性质
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)由奇函数的性质,f(0)=0,f(-1)=-f(1),得到a,b的方程,即可得到f(x);
(2)解关于x的指数不等式,注意运用指数函数的单调性,即可得到.
(2)解关于x的指数不等式,注意运用指数函数的单调性,即可得到.
解答:
解:(1)由于定义域为R的函数f(x)=
是奇函数,
则f(0)=0,即有1-b=0,即b=1,
再由f(-1)=-f(1),即有
=-
,解得,a=2,
即有f(x)=
,f(-x)=
=
=-f(x),
则f(x)是奇函数,
则有f(x)=
;
(2)不等式f(x)>-
即为
>-
,
即为2x>
,即有x>-2.
则所求x的取值集合为{x|x>-2}.
| 2x-b |
| 2x+1+a |
则f(0)=0,即有1-b=0,即b=1,
再由f(-1)=-f(1),即有
| 2-1-1 |
| 20+a |
| 2-1 |
| 22+a |
即有f(x)=
| 2x-1 |
| 2x+1+2 |
| 2-x-1 |
| 2(2-x+1) |
| 1-2x |
| 2(1+2x) |
则f(x)是奇函数,
则有f(x)=
| 2x-1 |
| 2x+1+2 |
(2)不等式f(x)>-
| 3 |
| 10 |
| 2x-1 |
| 2x+1 |
| 3 |
| 5 |
即为2x>
| 1 |
| 4 |
则所求x的取值集合为{x|x>-2}.
点评:本题考查函数的奇偶性的判断和运用,考查奇函数的性质,考查指数不等式的解法,属于基础题.

练习册系列答案
相关题目
两直线2x+3y-k=0和x+ky-12=0的交点在y轴上,那么k的值是( )
| A、-24 | B、6 | C、±6 | D、24 |
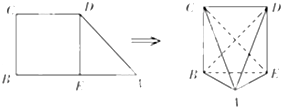 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE折叠.使四边形BCDE所在的平面与平面ADE垂直.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE折叠.使四边形BCDE所在的平面与平面ADE垂直. 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=