题目内容
函数f(x)=ax3+bx2+cx,设两个极值点是x=-1和x=1,求a,b,c的值.
考点:利用导数研究函数的极值
专题:导数的概念及应用
分析:本题可以先求出函数f(x)=ax3+bx2+cx的导函数f′(x),再利用函数f(x)=ax3+bx2+cx的两个极值点是x=-1和x=1,得到∴-1,1是方程3ax2+2bx+c=0的两个不相等的实数根,由根与系数的关系,求出a、b、c满足的关系,得到本题结论.
解答:
解:∵函数f(x)=ax3+bx2+cx,
∴f′(x)=3ax2+2bx+c.
∵函数f(x)=ax3+bx2+cx的两个极值点是x=-1和x=1,
∴-1,1是方程3ax2+2bx+c=0的两个不相等的实数根,
∴
,
∴b=0,c=-3a,a≠0.
经检验,适合题意.
∴∴b=0,c=-3a,a≠0.
∴f′(x)=3ax2+2bx+c.
∵函数f(x)=ax3+bx2+cx的两个极值点是x=-1和x=1,
∴-1,1是方程3ax2+2bx+c=0的两个不相等的实数根,
∴
|
∴b=0,c=-3a,a≠0.
经检验,适合题意.
∴∴b=0,c=-3a,a≠0.
点评:本题考查了导函数与极值点的关系,注意等价变形,或者要检验,本题难度不大,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
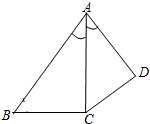 在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=
在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=