题目内容
求证:△ABC的外心S,重心G,垂心H在一条直线上,且G分
得比为2:1.
| HS |
考点:三角形五心
专题:平面向量及应用
分析:分析:根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得
=
+
,由向量相等和向量的减法运算进行转化,得到
+
+
=
,再根据△ABC重心为G满足
+
+
=
,结合已知中
+
+
=
,我们易判断出
=3
,根据数乘向量的几何意义,即可得到S,G,H三点共线,且G分
得比为2:1.
| SH |
| SA |
| AH |
| SA |
| SB |
| SC |
| SH |
| GA |
| GB |
| GC |
| 0 |
| SA |
| SB |
| SC |
| SH |
| SH |
| SG |
| HS |
解答:
解:如图:作直径BD,连接DA、DC,
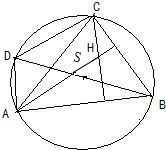
由图得,
=-
,
∵H为△ABC的垂心,
∴CH⊥AB,AH⊥BC,
∵BD为直径,
∴DA⊥AB,DC⊥BC
∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,
∴
=
,
又∵
=
-
=
+
,
∴
=
+
=
+
=
+
+
,
又∵G为△ABC的重心
∴
+
+
=(
+
)+(
+
)+(
+
)=3
+
+
+
=3
+
=
,
即
=3
,
即S,G,H三点共线,且SH=3SG
即S,G,H三点共线,且OG:GH=1:2.
从而得到:△ABC的外心S,重心G,垂心H在一条直线上,且G分
得比为2:1.

由图得,
| SB |
| SD |
∵H为△ABC的垂心,
∴CH⊥AB,AH⊥BC,
∵BD为直径,
∴DA⊥AB,DC⊥BC
∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,
∴
| AH |
| DC |
又∵
| DC |
| SC |
| SD |
| SC |
| SB |
∴
| SH |
| SA |
| AH |
| SA |
| DC |
| SA |
| SB |
| SC |
又∵G为△ABC的重心
∴
| GA |
| GB |
| GC |
| GS |
| SA |
| GS |
| SB |
| GS |
| SC |
| GS |
| SA |
| SB |
| SC |
| GS |
| SH |
| 0 |
即
| SH |
| SG |
即S,G,H三点共线,且SH=3SG
即S,G,H三点共线,且OG:GH=1:2.
从而得到:△ABC的外心S,重心G,垂心H在一条直线上,且G分
| HS |
点评:本题考查的知识点是三角形的五心,其中熟练掌握向量五心的向量表达式形式,如(1)中△ABC外心为O满足|
|=|
|=|
|,(2)中△ABC重心为G满足
+
+
=
,是解答此类问题的关键.
| OA |
| OB |
| OC |
| GA |
| GB |
| GC |
| 0 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)=
,则f′(
)等于( )
| sinx |
| sinx+cosx |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|