题目内容
甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一、乙不值周六,则可排出不同的值班表数为( )
| A、30 | B、42 | C、48 | D、60 |
考点:计数原理的应用
专题:排列组合
分析:先排甲乙,而甲若排在星期六,则乙就没有限制,所以可按甲的排法分类,分为两类,甲排在星期六,有C41C42种排法,甲不排在星期六,则甲从星期二到星期五之间选一天,有C42种选法,再排乙,不能安排在星期六,所以从剩下的3天中选2天,有C32种选法,最后排丙,再把两类相加即可.
解答:
解:由题意知本题是一个排列组合及简单计数问题,
根据题意分两类
当甲排在星期六,有C41C42=24种排法;
当甲不排在星期六,有C42C32=18种排法;
∴值班方案种数为24+18=42种.
故选:B.
根据题意分两类
当甲排在星期六,有C41C42=24种排法;
当甲不排在星期六,有C42C32=18种排法;
∴值班方案种数为24+18=42种.
故选:B.
点评:本题考查排列组合及简单的计数问题,本题解题的关键是可以从正面来解题,关键是如何分类.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,且a1=1,a2=3,若对任意n∈N*,都有an+2-an=2成立,则S100=( )
| A、2550 | B、2600 |
| C、5050 | D、5100 |
已知向量
=(4cos(
x+
),sinx),
=(sin(
x+
),sinx),定义函数f(x)=
•
+cos2x.若f(α)=2,且14≤α≤18,则tan(απ)的值为( )
| a |
| π |
| 16 |
| π |
| 8 |
| b |
| π |
| 16 |
| π |
| 8 |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
由a1=1,d=3确定的等差数列{an},当an=295时,序号n等于( )
| A、98 | B、99 | C、95 | D、100 |
如图程序运行后,输出的结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
定积分
cosxdx=( )
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
曲线y=x3+x2+x+1在点(-1,0)处的切线与抛物线y=ax2(a≠0)相切,则抛物线的准线方程是( )
A、y=-
| ||
B、y=
| ||
C、x=-
| ||
D、x=
|
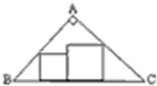 从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为
从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为