题目内容
2.如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F.已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE-BCF,如图2.
(Ⅰ)若AF⊥BD,证明:△BDE为直角三角形;
(Ⅱ)若DE∥CF,$CD=\sqrt{3}$,求平面ADC与平面ABFE所成角的余弦值.
分析 (1)由AF⊥BE,AF⊥BD可得AF⊥平面BFE,得出AF⊥DE,结合DE⊥AE即可得出DE⊥平面ABFE,故而DE⊥BE;
(2)求出∠CFE的大小,以E为原点建立空间坐标系,求出平面ACD和平面ABFE的法向量,计算两法向量的夹角即可得出二面角的大小.
解答 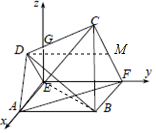 (1)证明:连接BE,
(1)证明:连接BE,
由已知可知四边形ABFE是正方形,∴AF⊥BE,
又AF⊥BD,BE∩DE=E,
∴AF⊥平面BDE,又DE?平面BDE,
∴AF⊥DE,
又DE⊥AE,AE∩AF=F,
∴DE⊥平面ABFE,又BE?平面ABFE,
∴DE⊥BE,即△BDE为直角三角形.
(2)取CF的中点M,连结DM,则四边形DEFM是平行四边形,
∴DM=EF=2,CM=$\frac{1}{2}$CF=1,又CD=$\sqrt{3}$,
∴cos∠CMD=$\frac{1+4-3}{2×1×2}$=$\frac{1}{2}$,即∠CMD=∠CFE=60°,
过E作EG⊥EF,则EG⊥平面ABFE,
以E为原点,以EA,EF,EG为坐标轴建立空间直角坐标系,
则A(2,0,0),C(0,1,$\sqrt{3}$),D(0,-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AC}$=(-2,1,$\sqrt{3}$),$\overrightarrow{AD}$=(-2,-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
设平面ACD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-2x+y+\sqrt{3}z=0}\\{-2x-\frac{1}{2}y+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,令z=$\sqrt{3}$得$\overrightarrow{n}$=(1,-1,$\sqrt{3}$),
又GE⊥平面ABFE,∴$\overrightarrow{m}$=(0,0,1)是平面ABFE的一个法向量,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{5}}$=$\frac{\sqrt{15}}{5}$,
由图形可知平面ADC与平面ABFE所成角为锐二面角,
∴平面ADC与平面ABFE所成角的余弦值为$\frac{\sqrt{15}}{5}$.
点评 本题考查了线面垂直的判定,空间向量与二面角的计算,属于中档题.

 习题精选系列答案
习题精选系列答案 已知函数f(x)=$\frac{4}{3}$x3-ax,在x=$\frac{1}{2}$处取得极小值,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{12}{25}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=$\frac{4}{3}$x3-ax,在x=$\frac{1}{2}$处取得极小值,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{12}{25}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤12? | B. | n>12? | C. | n≤13? | D. | n>13? |
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 阅读如图的框图,则输出的S=( )
阅读如图的框图,则输出的S=( )| A. | 30 | B. | 29 | C. | 55 | D. | 54 |