题目内容
已知函数y=|8-2x-x2|和y=kx+k(k为常数),则不论k为何常数,这两个函数图象的交点个数恒为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:函数的图象
专题:函数的性质及应用
分析:首先画出二次函数的图象,一次函数与x轴一定经过点(-1,0),根据图象即可确定交点的个数.
解答:
 解:函数y=8-2x-x2中,令y=0,解得:x=-4或2.
解:函数y=8-2x-x2中,令y=0,解得:x=-4或2.
则二次函数与x轴的交点坐标是(-4,0)和(2,0).则函数的图象如图.
一次函数y=kx+k(k为常数)中,令y=0,解得:x=-1,故这个函数一定经过点(-1,0).
经过(-1,0)的直线无论k为何常数,都是2个交点.
故选:B.
 解:函数y=8-2x-x2中,令y=0,解得:x=-4或2.
解:函数y=8-2x-x2中,令y=0,解得:x=-4或2.则二次函数与x轴的交点坐标是(-4,0)和(2,0).则函数的图象如图.
一次函数y=kx+k(k为常数)中,令y=0,解得:x=-1,故这个函数一定经过点(-1,0).
经过(-1,0)的直线无论k为何常数,都是2个交点.
故选:B.
点评:本题主要考查了一次函数与二次函数的图象,正确作出二次函数的答题图象,确定一次函数比经过(-1,0),利用数形结合思想是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=-2x+ax3,若f′(2)=1,则a=( )
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
如图,已知长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,则二面角B1-AC-B的余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若
(2x-3x2)dx=0,则k=( )
| ∫ | k 0 |
| A、1 | B、0 |
| C、0或1 | D、以上都不对 |
| sin2600° |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
判定下列命题
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
-
=
④(
•
)•
=
•(
•
)
正确的为( )
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
| AB |
| AC |
| CB |
④(
| a |
| b |
| c |
| a |
| b |
| c |
正确的为( )
| A、①② | B、①③ | C、②③ | D、①④ |
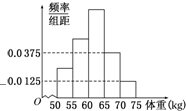 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )