题目内容
已知四棱锥DM如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.
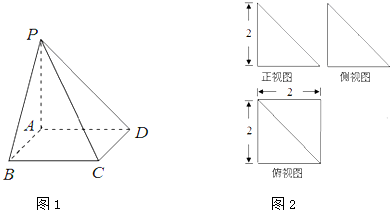
(1)若E是PD的中点,求证:AE⊥平面PCD;
(2)求此四棱锥的表面积.

(1)若E是PD的中点,求证:AE⊥平面PCD;
(2)求此四棱锥的表面积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:(1)通过证明AE⊥CD,AE⊥PD,利用直线与平面垂直的判定定理证明AE⊥平面PCD.
(2)求出底面面积SABCD=2×2=4,和高h=2,然后亲姐姐侧面积,即可求解四棱锥P-ABCD的表面积.
(2)求出底面面积SABCD=2×2=4,和高h=2,然后亲姐姐侧面积,即可求解四棱锥P-ABCD的表面积.
解答:
(1)证明:由三视图可知,PA⊥平面ABCD,∴CD⊥PA
∵ABCD是正方形,∴CD⊥AD
又PA∩AD=A,PA?平面ABCD,AD?平面ABCD,
∴CD⊥平面PAD,
∵AE?平面PAD,∴AE⊥CD
又△PAD是等腰直角三角形,E为PD的中点,∴AE⊥PD
又PD∩CD=D,PD?平面PCD,CD?平面PCD,
∴AE⊥平面PCD…(7分)
(2)解:由题意可知,四棱锥P-ABCD的底面是边长为2的正方形,
其面积SABCD=2×2=4,高h=2,斜高PB=PD=2
.
所以四棱锥P-ABCD的表面积S=2•2+
•2•2+
•2•2+
•2•2
+
•2•2
=8+4
…(13分)
∵ABCD是正方形,∴CD⊥AD
又PA∩AD=A,PA?平面ABCD,AD?平面ABCD,
∴CD⊥平面PAD,
∵AE?平面PAD,∴AE⊥CD
又△PAD是等腰直角三角形,E为PD的中点,∴AE⊥PD
又PD∩CD=D,PD?平面PCD,CD?平面PCD,
∴AE⊥平面PCD…(7分)
(2)解:由题意可知,四棱锥P-ABCD的底面是边长为2的正方形,
其面积SABCD=2×2=4,高h=2,斜高PB=PD=2
| 2 |
所以四棱锥P-ABCD的表面积S=2•2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查张筱雨平面垂直的判定定理的应用,几何体的表面积的求法,考查计算能力.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知函数f(x)=ax2+bx-2,(a>0,b∈R)的一个零点在区间(1,2)内,则a-b的取值范围是( )
| A、(-∞,-4) |
| B、(-4,+∞) |
| C、(-∞,2) |
| D、(-2,+∞) |
下列说法正确的是( )
| A、命题“若x=1则x2=1”的否命题为“若x2≠1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、“命题p,q中至少有一个为真命题”是“p或q为真命题”的充分不必要条件 |
已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=
,则椭圆和双曲线的离心率的乘积的最小值为( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知圆C的方程是x2+y2-8x-2y+10=0,过点M(3,0)的最短弦所在的直线方程是( )
| A、x+y-3=0 |
| B、x-y-3=0 |
| C、2x-y-6=0 |
| D、2x+y-6=0 |