题目内容
在Rt△ABC中,AC⊥BC,AC=a,BC=b,则△ABC的外接圆半径r=
;类比到空间,若三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为a、b、c,则三棱锥S-ABC的外接球的半径R= .
| ||
| 2 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离,推理和证明,球
分析:直角三角形外接圆半径为斜边长的一半,由类比推理可知若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,将三棱锥补成一个长方体,其外接球的半径R为长方体对角线长的一半.
解答:
解:若三棱锥三条侧棱两两垂直,侧棱长分别为a,b,c,
可补成一个长方体,体对角线长为
,
∵体对角线就是外接球的直径,
∴棱锥的外接球半径R=
.
故答案为:
.
可补成一个长方体,体对角线长为
| a2+b2+c2 |
∵体对角线就是外接球的直径,
∴棱锥的外接球半径R=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查球与内接三棱锥的位置关系,考查球的半径的求法,考查类比思想的运用,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 执行如图所示的程序框图,若输入的n值等于7,则输出s的值为( )
执行如图所示的程序框图,若输入的n值等于7,则输出s的值为( )| A、15 | B、16 | C、21 | D、22 |
已知函数f(x)=x+sinπx-3,则f(
)+f(
)+f(
)+…+f(
)的值为( )
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4029 |
| 2015 |
| A、4029 | B、-4029 |
| C、8058 | D、-8058 |
已知f(x)=x3+2x,则f(5)+f(-5)的值是( )
| A、-1 | B、0 | C、1 | D、2 |
设函数f(x)=sinωx+cosωx(ω>0)的最小正周期为π,将y=f(x)的图象向左平移
个单位得函数y=g(x)的图象,则( )
| π |
| 8 |
A、g(x)在(0,
| ||||
B、g(x)在(
| ||||
C、g(x)在(0,
| ||||
D、g(x)在(
|
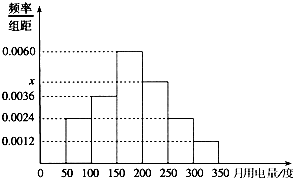
 从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.
从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图所示.