题目内容
复数集中,一个数的平方恰好为这个数的共轭复数的数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:利用复数的运算法则、共轭复数的定义、复数相等即可得出.
解答:
解:设z=a+bi,(a,b∈R),
则z2=
,∴(a+bi)2=a-bi,
∴a2-b2+2abi=a-bi,
∴
,
解得
,
,
∴z=0,1,-
±
i.
因此满足条件的复数z共有4个.
故选:A.
则z2=
. |
| z |
∴a2-b2+2abi=a-bi,
∴
|
解得
|
|
∴z=0,1,-
| 1 |
| 2 |
| ||
| 2 |
因此满足条件的复数z共有4个.
故选:A.
点评:本题考查了复数的运算法则、共轭复数的定义、复数相等,属于基础题.

练习册系列答案
相关题目
下列函数中,奇函数是( )
| A、f(x)=2x |
| B、f(x)=log2x |
| C、f(x)=sinx+1 |
| D、f(x)=sinx+tanx |
i是虚数单位,计算
=( )
| 1+i |
| 1-i |
| A、-1 | B、1 | C、i | D、-i |
若正数a,b满足ab=a+b+8,则ab的取值范围是( )
| A、(0,16] |
| B、[4,16) |
| C、[4,16] |
| D、[16,+∞) |
直线y-5=0的斜率为( )
| A、1 | B、0 | C、5 | D、不存在 |
已知命题p:“?a”的否定是“?x0<0,x02+x0-1≥0”;命题q:在△ABC中“∠A>∠B”的充要条件是“sinA>sinB”;则下列命题是假命题的是( )
| A、p∨q |
| B、p∨(?q) |
| C、(?p)∨q |
| D、(?p)∨(?q) |
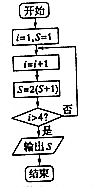 在如图所示的程序框图表示的算法中,输出的结果是
在如图所示的程序框图表示的算法中,输出的结果是