题目内容
若椭圆
+
=1(a>b>0)的离心率e为黄金分割比
,则称该椭圆为“优美椭圆”,该类椭圆具有性质b2=ac(c为该椭圆的半焦距).那么在双曲线
-
=1(a>0,b>0)中具有类似性质的“优美双曲线”的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先根据信息的要求建立等量关系,通过离心率的转化求出结果.
解答:
解:根据题意具有优美双曲线的性质为:b2=ac
则:c2-a2=ac
整理得:c2-a2-ac=0
进一步得:(
)2-
-1=0
即:e2-e-1=0
解得:e=
由于双曲线的离心率e>1
所以:e=
故选:B
则:c2-a2=ac
整理得:c2-a2-ac=0
进一步得:(
| c |
| a |
| c |
| a |
即:e2-e-1=0
解得:e=
1±
| ||
| 2 |
由于双曲线的离心率e>1
所以:e=
1+
| ||
| 2 |
故选:B
点评:本题考查的知识要点:双曲线离心率的应用.属于基础题型.

练习册系列答案
相关题目
圆x2+y2+2x-6y-15=0与直线(1+3m)x+(3-2m)y+4m-17=0的交点个数是( )
| A、2 | B、1 | C、0 | D、与m有关 |
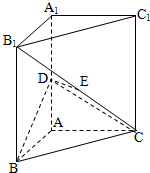 如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.
如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.