题目内容
15.在△ABC中,已知c-b=1,bc=30,S△=$\frac{15}{2}$,求∠A和a.分析 c-b=1,bc=30,解得c=6,b=5.再利用三角形面积计算公式可得A,利用勾股定理可得a.
解答 解:∵c-b=1,bc=30,∴c=6,b=5.
∵S△=$\frac{15}{2}$,∴$\frac{1}{2}bcsinA$=$\frac{1}{2}×30×$sinA=$\frac{15}{2}$,可得sinA=1,A∈(0,π),解得A=$\frac{π}{2}$.
∴a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{61}$.
点评 本题考查了三角形面积计算公式、勾股定理、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.若y=f(x)是定义域在R上的函数,则y=f(x)为奇函数的一个充要条件为( )
| A. | f(0)=0 | B. | 对?x∈R,f(x)=0都成立 | ||
| C. | ?x0∈R,使得f(x0)+f(-x0)=0 | D. | 对?x∈R,f(x)+f(-x)=0都成立 |
3.设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$,其中a为常数,当且仅当x=y=1时,目标函数z=x+2y取得最小值,则目标函数z的最大值为( )
| A. | 8 | B. | $\frac{27}{5}$ | C. | 6 | D. | 3 |
20.若函数f(x)与函数g(x)的奇偶性相同,则称g(x)为f(x)的同心函数.那么,在下列给出的函数中,为函数f(x)=$\frac{{{x^2}-1}}{x}$的同心函数的是( )
| A. | g(x)=x+1 | B. | g(x)=2x | C. | g(x)=x2 | D. | g(x)=lnx |
7.如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图,其中 ①②分别是( )
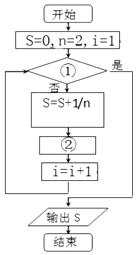

| A. | i<30,n=n+2 | B. | i>30,n=n+2 | C. | i<30,n=n+1 | D. | i>30,n=n+1 |