题目内容
6.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).(1)若$\frac{c}{b}=\sqrt{3}$,求角A;
(2)在(1)的条件下,若△ABC的面积为$\sqrt{3}$,求a的值.
分析 (1)过B作BD⊥AC,则b=acosC+ccosA,结合条件可得3bsinA=ccosA,得出tanA;
(2)根据面积公式和$\frac{c}{b}=\sqrt{3}$计算b,c,再利用余弦定理得出a.
解答 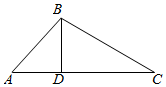 解:(1)在△ABC中,过B作BD⊥AC,则b=AD+CD=acosC+ccosA.
解:(1)在△ABC中,过B作BD⊥AC,则b=AD+CD=acosC+ccosA.
∵b=acosC+3bsin(B+C)=acosC+3bsinA,
∴3bsinA=ccosA,∴$\frac{c}{b}$=3tanA=$\sqrt{3}$,
∴tanA=$\frac{\sqrt{3}}{3}$,A=$\frac{π}{6}$.
(2)∵S△ABC=$\frac{1}{2}bc$sinA=$\frac{1}{4}bc$=$\sqrt{3}$,
∴bc=4$\sqrt{3}$,
∵c=$\sqrt{3}b$,∴b=2,c=2$\sqrt{3}$.
由余弦定理得a2=b2+c2-2bccosA=4+12-12=4.
∴a=2.
点评 本题考查了,余弦定理,三角形的面积公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.△ABC的三个内角A,B,C所对的边分别是a,b,c,若$a=2,c=\sqrt{19}$,$tanA+tanB=\sqrt{3}-\sqrt{3}tanAtanB$,则△ABC的面积S△ABC=( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
11.已知菱形ABCD的边长为4,$∠ABC=\frac{π}{6}$,若在菱形内取一点,则该点到菱形的四个顶点的距离均大于1的概率为( )
| A. | $\frac{π}{4}$ | B. | $1-\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $1-\frac{π}{8}$ |
15.点P到图形C上所有点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C的距离与到圆C外的定点A的距离相等的点的轨迹是( )
| A. | 射线 | B. | 椭圆 | C. | 双曲线的一支 | D. | 抛物线 |