题目内容
已知函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,则m+2n的取值范围为 .
考点:一元二次方程的根的分布与系数的关系
专题:计算题,函数的性质及应用
分析:由两个零点分别在区间(-1,2)和(2,3)内,根据零点存在定理,我们易得:f(-1)<0,f(2)>0,f(3)<0,由此我们易构造一个平面区域,利用线性规划知识即可求出答案.
解答:
 解:∵函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,
解:∵函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,
∴f(-1)<0,f(2)>0,f(3)<0,
∴
,
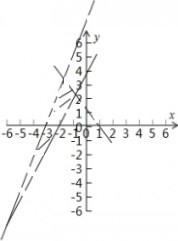
平面区域如图所示,三个交点坐标分别为(-1,2),(-2,3),(-5,-6),
∴m+2n在(-2,3)处取得最大值4,在(-5,-6)处取得最小值为-17,
∴m+2n的取值范围为(-17,4).
故答案为:(-17,4).
 解:∵函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,
解:∵函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,∴f(-1)<0,f(2)>0,f(3)<0,
∴
|
平面区域如图所示,三个交点坐标分别为(-1,2),(-2,3),(-5,-6),
∴m+2n在(-2,3)处取得最大值4,在(-5,-6)处取得最小值为-17,
∴m+2n的取值范围为(-17,4).
故答案为:(-17,4).
点评:本题考查的知识点是函数零点的求法及零点存在定理,其中连续函数在区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点,是判断函数零点存在最常用的方法.

练习册系列答案
相关题目
已知向量
=(sinα,cos2α),
=(1-2sinα,-1),α∈=(
,
),若
•
=-
,则tanα的值为( )
| a |
| b |
| π |
| 2 |
| 3π |
| 2 |
| a |
| b |
| 8 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
