题目内容
 如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.(1)设FC的中点为M,求证:OM∥面DAAF;
(2)求证:AF⊥面CBF.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间向量及应用
分析:(1)先证明OM∥AN,根据线面平行的判定定理即可证明OM∥面DAF;
(2)由题意可先证明AF⊥CB,由AB为圆O的直径,可证明AF⊥BF,根据线面垂直的判定定理或面面垂直的性质定理即可证明AF⊥面CBF.
(2)由题意可先证明AF⊥CB,由AB为圆O的直径,可证明AF⊥BF,根据线面垂直的判定定理或面面垂直的性质定理即可证明AF⊥面CBF.
解答:
解:(1)设DF的中点为N,连接MN,
则MN∥
CD,MN=
CD,
又∵AO∥
CD,AO=
CD,
∴MN∥AO,MN=AO,
∴MNAO为平行四边形,
∴OM∥AN.
又∵AN?面DAF,OM?面DAF,
∴OM∥面DAF.
(2)∵面ABCD⊥面ABEF,CB⊥AB,CB?面ABCD,面ABCD∩面ABEF=AB,
∴CB⊥面ABEF.
∵AF?面ABEF,
∴AF⊥CB.
又∵AB为圆O的直径,
∴AF⊥BF,
又∵CB∩BF=B,CB,BF?面CBF.
∴AF⊥面CBF.
则MN∥
| 1 |
| 2 |
| 1 |
| 2 |
又∵AO∥
| 1 |
| 2 |
| 1 |
| 2 |
∴MN∥AO,MN=AO,
∴MNAO为平行四边形,
∴OM∥AN.
又∵AN?面DAF,OM?面DAF,
∴OM∥面DAF.
(2)∵面ABCD⊥面ABEF,CB⊥AB,CB?面ABCD,面ABCD∩面ABEF=AB,
∴CB⊥面ABEF.
∵AF?面ABEF,
∴AF⊥CB.
又∵AB为圆O的直径,
∴AF⊥BF,
又∵CB∩BF=B,CB,BF?面CBF.
∴AF⊥面CBF.
点评:本题主要考查了平面与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和转化思想,属于中档题.

练习册系列答案
相关题目
 是定义在
是定义在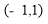 上的奇函数,且
上的奇函数,且 ,
,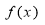 的解析式;
的解析式; 在
在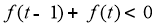 .
.
 平行,则它们之间的距离是( )
平行,则它们之间的距离是( ) D.4
D.4